题目内容
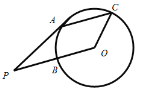
【题目】如图,已知![]() 是
是![]() 的切线,
的切线,![]() 为切点,
为切点,![]() 与
与![]() 相交于
相交于![]() 点,B为
点,B为![]() 的中点,
的中点,![]() 为
为![]() 上一点,
上一点,![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
连接AB、OA,如图,先利用切线的性质得∠OAP=90°,再根据斜边上的中线等于斜边的一半判断△OAB为等边三角形,则∠AOP=60°,接着利用平行线的性质得到∠AOP=∠OAC=60°,则∠AOC=60°,然后计算∠PAC+∠POC.
解:连接AB、OA,如图,
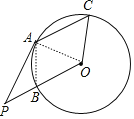
∵PA是⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
∵B为OP的中点,
∴AB=BP=BO,
∴△OAB为等边三角形,
∴∠AOP=60°,
∵AC∥OP,
∴∠AOP=∠OAC=60°,
∴△OAC为等边三角形,
∴∠AOC=60°,
∴∠PAC+∠POC=90°+60°+60°+60°=270°.
故选D.

练习册系列答案
相关题目
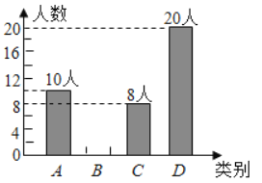
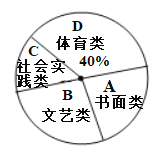
【题目】从2018年12月初开始,某地环保部门连续一年对![]() 两市的空气质量进行监测,将
两市的空气质量进行监测,将![]() 天的空气污染指数(简称:API)的平均值作为每个月的空气污染指数,
天的空气污染指数(简称:API)的平均值作为每个月的空气污染指数,![]() 个月的空气污染指数如下:
个月的空气污染指数如下:
![]()
![]()
整理、描述数据:
空气质量
按如表整理、描述这两市空气污染指数的数据:
城市 | 空气质量为优 | 空气质量为良 | 空气质量为轻微污染 |
|
|
|
|
|
说明:空气污染指数![]() 时,空气质量为优;
时,空气质量为优;![]() 空气污染指数
空气污染指数![]() 时,空气质量为良;
时,空气质量为良;![]() 空气污染指数
空气污染指数![]() 时,空气质量为轻微污染.
时,空气质量为轻微污染.
分析数据:
两市的空气污染指数的平均数、中位数、众数如下表所示;
城市 | 平均数 | 中位数 | 众数 |
|
|
| |
|
|
|
请将以上两个表格补充完整:
得出结论:可以推断出 市这一年中环境状况比较好,理由_____.(至少从两个不同的角度说明推断的合理性)