题目内容
【题目】已知关于x的方程x2﹣（k+1）x+
k2+1=0有两个实数根．
（1）求k的取值范围；
（2）若方程的两实数根分别为x1，x2，且x12+x22=6x1x2﹣15，求k的值．
【答案】（1）k≥
；（2）4
【解析】
（1）根据判别式与根的个数之间的关系，列不等式计算即可；
（2）根据一元二次方程根与系数间的关系表示出
，
，再由
代入进行计算即可．
解：（1）由题意，得△=[﹣（k+1）]2﹣4（
k2+1）=2k﹣3≥0，
解得
，
∴k的取值范围为k≥．
（2）∵由根与系数的关系，得x1+x2=k+1，x1x2=k2+1 ，
∵x12+x22=6x1x2﹣15，
∴（x1+x2）2﹣8x1x2+15=0，
∴k2﹣2k﹣8=0，解得：k1=4，k2=﹣2 ，
又∵k≥，
∴k=4．
练习册系列答案
相关题目
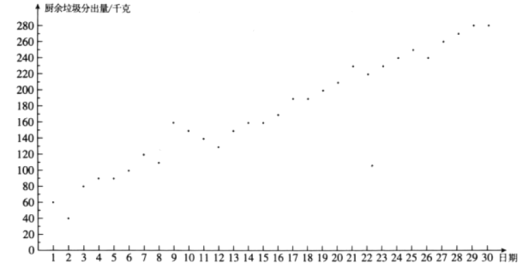
【题目】小云统计了自己所住小区5月1日至30日的厨余垃圾分出量（单位：千克），相关信息如下：
．小云所住小区5月1日至30日的厨余垃圾分出量统计图：
．小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下：
时段 | 1日至10日 | 11日至20日 | 21日至30日 |
平均数 | 100 | 170 | 250 |
（1）该小区5月1日至30日的厨余垃圾分出量的平均数约为 （结果取整数）
（2）已知该小区4月的厨余垃圾分出量的平均数为60，则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的 倍（结果保留小数点后一位）；
（3）记该小区5月1日至10日的厨余垃圾分出量的方差为
5月11日至20日的厨余垃圾分出量的方差为
，5月21日至30日的厨余垃圾分出量的方差为
．直接写出
的大小关系．
