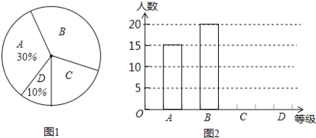
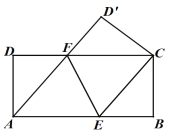
题目内容
【题目】如图,宾馆大厅的天花板上挂有一盏吊灯AB,某人从C点测得吊灯顶端A的仰角为![]() ,吊灯底端B的仰角为
,吊灯底端B的仰角为![]() ,从C点沿水平方向前进6米到达点D,测得吊灯底端B的仰角为
,从C点沿水平方向前进6米到达点D,测得吊灯底端B的仰角为![]() .请根据以上数据求出吊灯AB的长度.(结果精确到0.1米.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,
.请根据以上数据求出吊灯AB的长度.(结果精确到0.1米.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
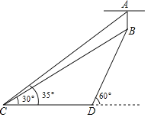
【答案】吊灯AB的长度约为1.1米.
【解析】
延长CD交AB的延长线于点E,构建直角三角形,分别在两个直角三角形△BDE和△AEC中利用正弦和正切函数求出AE长和BE长,即可求解.
解:延长CD交AB的延长线于点E,则∠AEC=90°,
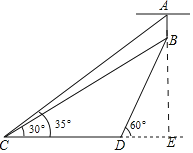
∵∠BDE=60°,∠DCB=30°,
∴∠CBD=60°﹣30°=30°,
∴∠DCB=∠CBD,
∴BD=CD=6(米)
在Rt△BDE中,sin∠BDE=![]() ,
,
∴BE=BDsin∠BDE═6×sin60°=3![]() ≈5.19(米),
≈5.19(米),
DE=![]() BD=3(米),
BD=3(米),
在Rt△AEC中,tan∠ACE=![]() ,
,
∴AE=CEtan∠ACE=(6+3)×tan35°≈9×0.70=6.30(米),
∴AB=AE﹣BE≈6.30﹣5.19≈1.1(米),
∴吊灯AB的长度约为1.1米.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目