Question

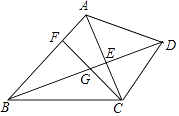
【题目】已知：如图，在△ABC中，AB=AC，过点A作AD⊥BC，垂足为点D，延长AD至点E，使DE= AD，过点A作AF∥BC，交EC的延长线于点F．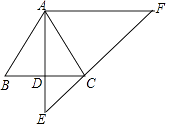
（1）设 = ， = ，用 、 的线性组合表示 ；
（2）求 的值．

Answer 1

【答案】
（1）解：∵如图，在△ABC中，AB=AC，AD⊥BC，

∴BD= BC，

∵ = ， = ，

∴ = + = + ．

又∵DE= AD，

∴ = = + ，

∴ = + = + + + = +

（2）解：∵DE= AD，AF∥BC，

∴ = ， = = ，

∴ = = = × = ，

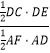即 = ．

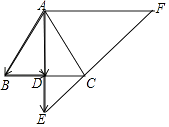
【解析】（1）由平面向量的三角形法则得到 ，然后结合已知条件DE= AD来求 ；（2）根据平行线截线段成比例和三角形的面积公式进行解答．根据平行线截线段成比例和三角形的面积公式进行解答．
【考点精析】关于本题考查的等腰三角形的性质，需要了解等腰三角形的两个底角相等（简称：等边对等角）才能得出正确答案．