题目内容
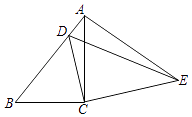
【题目】已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GEGD. 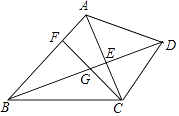
(1)求证:∠ACF=∠ABD;
(2)连接EF,求证:EFCG=EGCB.
【答案】
(1)证明:∵CG2=GEGD,
∴ ![]() .
.
又∵∠CGD=∠EGC,
∴△GCD∽△GEC.
∴∠GDC=∠GCE.
∵AB∥CD,
∴∠ABD=∠BDC.
∴∠ACF=∠ABD.
(2)证明:∵∠ABD=∠ACF,∠BGF=∠CGE,
∴△BGF∽△CGE.
∴ ![]() .
.
又∵∠FGE=∠BGC,
∴△FGE∽△BGC.
∴ ![]() .
.
∴FECG=EGCB.
【解析】(1)先根据CG2=GEGD得出 ![]() ,再由∠CGD=∠EGC可知△GCD∽△GEC,∠GDC=∠GCE.根据AB∥CD得出∠ABD=∠BDC,故可得出结论;(2)先根据∠ABD=∠ACF,∠BGF=∠CGE得出△BGF∽△CGE,故
,再由∠CGD=∠EGC可知△GCD∽△GEC,∠GDC=∠GCE.根据AB∥CD得出∠ABD=∠BDC,故可得出结论;(2)先根据∠ABD=∠ACF,∠BGF=∠CGE得出△BGF∽△CGE,故 ![]() .再由∠FGE=∠BGC得出△FGE∽△BGC,进而可得出结论.
.再由∠FGE=∠BGC得出△FGE∽△BGC,进而可得出结论.

练习册系列答案
相关题目