题目内容
【题目】如图，矩形ABCD中，M为CD中点，分别以B、M为圆心，以BC长、MC长为半径画弧，两弧相交于点P，若∠PBC=70°，则∠MPC的度数为（ ）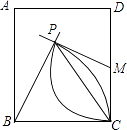 
A.55°
B.40°
C.35°
D.20°
【答案】C
【解析】解：∵以B、M为圆心，分别以BC长、MC长为半径的两弧相交于P点， ∴BP=BC，MP=MC，
∵∠PBC=70°，
∴∠BCP= 
（180°﹣∠PBC）= （180°﹣70°）=55°，
在长方形ABCD中，∠BCD=90°，
∴∠MCP=90°﹣∠BCP=90°﹣55°=35°，
∴∠MPC=∠MCP=35°．
故选：C．
根据BP=BC，MP=MC，∠PBC=70°，得出∠BCP= （180°﹣∠PBC），再根据∠BCD=90°，得出∠MCP=90°﹣∠BCP=35°，进行计算即可．
练习册系列答案
相关题目
