题目内容
【题目】如图，在平面直角坐标系xOy中，抛物线y=ax2+bx+4与x轴的正半轴相交于点A，与y轴相交于点B，点C在线段OA上，点D在此抛物线上，CD⊥x轴，且∠DCB=∠DAB，AB与CD相交于点E．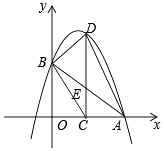
（1）求证：△BDE∽△CAE；
（2）已知OC=2，tan∠DAC=3，求此抛物线的表达式．
【答案】
（1）
证明：∵∠DCB=∠DAB，∠BEC=∠DEA，
∴△BEC∽△DEA，
∴ 
= 
，又∠BED=∠CEA，
∴△BDE∽△CAE；
（2）
解：∵抛物线y=ax2+bx+4与y轴相交于点B，
∴点B的坐标为（0，4），即OB=4，
∵tan∠DAC=3，
∴ 
=3，
设AC=m，则DC=3m，OA=m+2，
则点A的坐标为（m+2，0），点D的坐标为（2，3m），
∵△BDE∽△CAE，
∴∠DBA=∠DCA=90°，
∴BD2+BC2=CD2，即22+（3m﹣4）2+（m+2）2+42=m2+（3m）2，
解得，m=2，
则点A的坐标为（4，0），点D的坐标为（2，6），
∴ 
，
解得， 
，
∴抛物线的表达式为y=﹣x2+3x+4
【解析】（1）根据相似三角形的判定定理得到△BEC∽△DEA，根据相似三角形的性质定理得到 = ，根据相似三角形的判定定理证明即可；（2）设AC=m，根据正切的定义得到DC=3m，根据相似三角形的性质得到∠DBA=∠DCA=90°，根据勾股定理列出算式，求出m的值，利用待定系数法求出抛物线的解析式．
【考点精析】根据题目的已知条件，利用二次函数的概念和二次函数的图象的相关知识可以得到问题的答案，需要掌握一般地，自变量x和因变量y之间存在如下关系：一般式：y=ax2+bx+c(a≠0，a、b、c为常数)，则称y为x的二次函数；二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点．
