题目内容
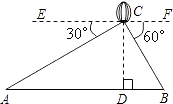
【题目】将两块全等的三角板如图①摆放，其中∠A1CB1=∠ACB=90°，∠A1=∠A=30°．
（1）将图①中的△A1B1C顺时针旋转45°得图②，点P1是A1C与AB的交点，点Q是A1B1与BC的交点，求证：CP1=CQ；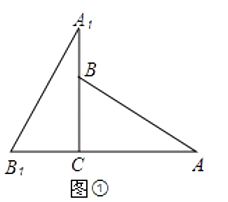
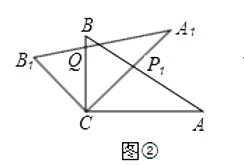
（2）在图②中，若AP1=2，则CQ等于多少？
（3）如图③，在B1C上取一点E，连接BE、P1E，设BC=1，当BE⊥P1B时，求△P1BE面积的最大值．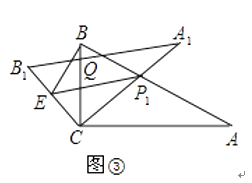
【答案】
（1）证明：∵∠B1CB=45°，∠B1CA1=90°，
∴∠B1CQ=∠BCP1=45°，
∵在△B1CQ和△BCP1中，
，
∴△B1CQ≌△BCP1（ASA），
∴CQ=CP1
（2）解：作P1D⊥CA于D，
∵∠A=30°，
∴P1D= 
AP1=1，
∵∠P1CD=45°，
∴ 
=sin45°= 
，
∴CP1= 
P1D= ，
又∵CP1=CQ，
∴CQ=
（3）解：∵∠P1BE=90°，∠ABC=60°，
∴∠A=∠CBE=30°，
∴AC= 
BC，
由旋转的性质可得：∠ACP1=∠BCE，
∴△AP1C∽△BEC，
∴AP1：BE=AC：BC= ：1，
设AP1=x，则BE= 
x，
在Rt△ABC中，∠A=30°，
∴AB=2BC=2，
∴S△P1BE= × x（2﹣x）=﹣ 
x2+ x
=﹣ （x﹣1）2+ ，
故当x=1时，S△P1BE（max）=
【解析】（1）根据旋转的性质，易证得△B1CQ≌△BCP1，即可得到CQ=CP1。
（2）由（1）结论可知CQ=CP1。要求CQ的长，只需求出CP1的长，添加辅助线，将CP1转化到直角三角形中，作P1D⊥CA于D，根据∠A=30°，可求出P1D的长，然后在Rt△P1DC中，可求出CP1的长，即可得出结论。
（3）根据旋转的性质，先证明△AP1C∽△BEC，得对应边成比例，建立方程，用含x的代数式分别表示出AP1、BE的长，在Rt△ABC中，求出AB的长，即可求出S△P1BE与x的函数关系式，求出顶点坐标，即可得到△P1BE面积的最大值。
【考点精析】根据题目的已知条件，利用二次函数的最值和相似三角形的判定与性质的相关知识可以得到问题的答案，需要掌握如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
