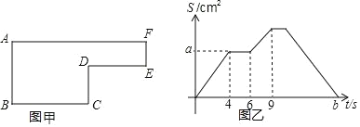
题目内容
【题目】如图,从热气球C上测得两建筑物A,B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A,D,B在同一直线上,求建筑物A,B间的距离.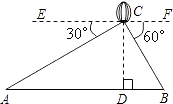
【答案】解:由已知,得∠ECA=30°,∠FCB=60°,CD=90,
EF∥AB,CD⊥AB于点D.
∴∠A=∠ECA=30°,∠B=∠FCB=60°.
在Rt△ACD中,∠CDA=90°,tanA= ![]() ,
,
∴AD= ![]() =90×
=90× ![]() =90
=90 ![]() .
.
在Rt△BCD中,∠CDB=90°,tanB= ![]() ,
,
∴DB= ![]() =30
=30 ![]() .
.
∴AB=AD+BD=90 ![]() +30
+30 ![]() =120
=120 ![]() .
.
答:建筑物A、B间的距离为120 ![]() 米
米
【解析】添加辅助线,将相关的问题转化到直角三角形中求解。过点C作CD⊥AB于点D,根据已知易求得∠A、∠B的度数,再在Rt△ACD和Rt△BCD中,分别求出DB、AD的长,就可以求出AB的长。
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法),以及对关于仰角俯角问题的理解,了解仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.

【题目】某饮料厂开发了A,B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A,B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
原料名称 | 甲 | 乙 |
A | 20克 | 40克 |
B | 30克 | 20克 |
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?