题目内容
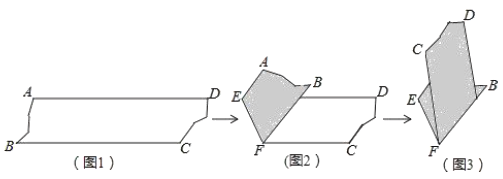
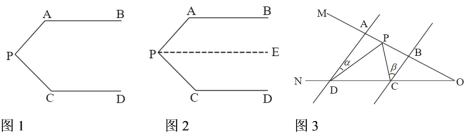
【题目】(1)同题情景:如图1,AB//CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明想到一种方法,但是没有解答完:
如图2,过P作PE//AB,∴∠APE+∠PAB=180°,
∴∠APE=180°-∠PAB=180°-130°=50°
∵AB//CD,∴PE//CD.
……
请你帮助小明完成剩余的解答.
(2)问题迁移:请你依据小明的解题思路,解答下面的问题:
如图3,AD//BC,当点P在A、B两点之间时,∠ADP=∠α,∠BCP=∠β,则∠CPD,∠α,∠β之间有何数量关系?请说明理由.
【答案】(1) 110°,剩余解答见解析;(2) ∠CPD=∠α+∠β,理由见解析
【解析】
(1)过P作PE∥AB,构造同旁内角,通过平行线性质,可得∠APC=50°+60°=110°
(2)过P作PE∥AD交CD于E点,推出AD∥PE∥BC,根据平行线性质得到∠α=∠DPE,∠β=∠CPE,即可得出答案.
解:(1)剩余过程:∠CPE+∠PCD=180°,
∴∠CPE=180°-120°=60°
∠APC=50°+60°=110°;
故答案为:110°.
(2)∠CPD=∠α+∠β,理由如下:
如下图,过P作PE∥AD交CD于点E,
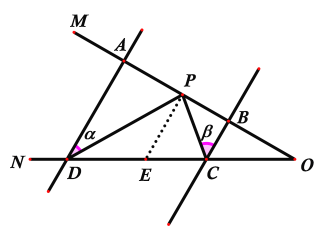
∵AD∥BC
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE
∴∠CPD=∠DPE+∠CPE=∠α+∠β
故答案为:∠CPD=∠α+∠β.

【题目】某饮料厂开发了A,B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A,B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
原料名称 | 甲 | 乙 |
A | 20克 | 40克 |
B | 30克 | 20克 |
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?