题目内容
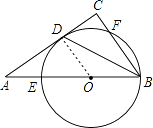
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB,BC于点E,F.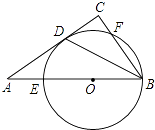
(1)求证:AC是⊙O的切线;
(2)已知AB=5,AC=4,求⊙O的半径r.
【答案】
(1)证明:连接OD,如图,
∵OB=OD,
∴∠ODB=∠OBD,
∵∠ABC的平分线交AC于点D,
∴∠OBD=∠DBC,
∴∠ODB=∠DBC,
∴OD∥BC,
∵∠C=90°,
∴∠ADO=90°,
∴OD⊥AC,
∴AC是⊙O的切线
(2)解:在Rt△ABC中,∵∠C=90°,AB=5,AC=4,
∴BC= ![]() =3,
=3,
∵OD∥BC,
∴△AOD∽△ABC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得r= ![]() .
.
【解析】要证AC是⊙O的切线,可知点D在圆上,因此连半径OD,再证明OD⊥AC即可,只需证出OD∥BC,再根据已知∠C=90°,即可得结论。
(2)在Rt△ABC中,利用勾股定理即可求出BC的长,再证明△AOD∽△ABC,运用相似三角形的性质,得对应边成比例,建立关于r的方程,求解即可。
【考点精析】本题主要考查了勾股定理的概念和切线的判定定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目