题目内容
【题目】某工厂生产一种产品，当生产数量至少为10吨，但不超过50吨时，每吨的成本y（万元/吨）与生产数量x（吨）的函数关系的图象如图所示．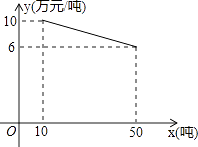
（1）求y关于x的函数解析式，并写出x的取值范围；
（2）当生产这种产品每吨的成本为7万元时，求该产品的生产数量．
【答案】
（1）解：设y=kx+b（k≠0），
由图可知，函数图象经过点（10，10），（50，6），则
，
解得 
．
故y=﹣ 
x+11（10≤x≤50）
（2）解：y=7时，﹣ x+11=7，
解得x=40．
答：每吨成本为7万元时，该产品的生产数量40吨
【解析】根据图像上点的坐标，函数图象经过点（10，10），（50，6），用待定系数法求出y关于x的函数解析式；（2）根据当生产这种产品每吨的成本为7万元时，代入求出x的值即可.
练习册系列答案
相关题目
【题目】某饮料厂开发了A，B两种新型饮料，主要原料均为甲和乙，每瓶饮料中甲、乙的含量如下表所示．现用甲原料和乙原料各2800克进行试生产，计划生产A，B两种饮料共100瓶．设生产A种饮料x瓶，解析下列问题：
原料名称 | 甲 | 乙 |
A | 20克 | 40克 |
B | 30克 | 20克 |
（1）有几种符合题意的生产方案写出解析过程；
（2）如果A种饮料每瓶的成本为2.60元，B种饮料每瓶的成本为2.80元，这两种饮料成本总额为y元，请写出y与x之间的关系式，并说明x取何值会使成本总额最低？
