题目内容
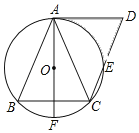
【题目】已知：AB为⊙O直径，弦CD⊥AB，垂足为H，点E为⊙O上一点，
，BE与CD交于点F．
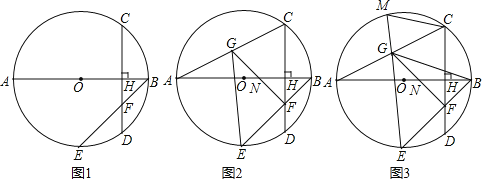
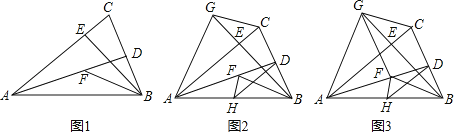
（1）如图1，求证：BH＝FH；
（2）如图2，过点F作FG⊥BE，分别交AC、AB于点G、N，连接EG，求证：EB＝EG；
（3）如图3，在（2）的条件下，延长EG交⊙O于M，连接CM、BG，若ON＝1，△CMG的面积为6，求线段BG的长．
【答案】（1）见解析；（2）见解析；（3）2
．
【解析】
（1）连接
，根据直径所对圆周角等于90°及弧与弦的关系即可得解；
（2）根据题意，过点C作
，连接
，通过证明
，
即可得解；
（3）根据题意，过点G作
于T，连接CN，设
，证明
，再由面积法及勾股定理进行计算求解即可.
解：（1）如下图，连接
∵
为直径
∴
∵
∴
∴
又∵
于H
∴
∴
；
（2）如下图，过点C作，连接
AB为直径，∴
∴
∴
∴
同理
∴
；
（3）如下图，过点G作于T，连接CN
设
由（2）知：
∴
∵
∴
∵
∴
∴
则：
∴
∴
∴
∵
面积为6
∴
设
则
∴
∴
∴
解得：
∵
∴
，则
∴
．
练习册系列答案
考前必练系列答案
相关题目
