题目内容
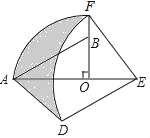
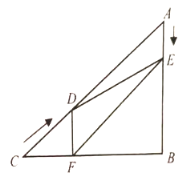
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时,动点
;同时,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动,另一个点也停止运动.设点
;当一个点停止运动,另一个点也停止运动.设点![]() ,
,![]() 运动的时间是
运动的时间是![]()
![]()
![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)![]() 为何值时,
为何值时,![]() ?
?
(2)设四边形![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)是否存在某一时刻![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)当![]() 为何值时,
为何值时,![]() ?
?
【答案】(1)当t=![]() 时,DE⊥AC;(2)
时,DE⊥AC;(2)![]() ;(3)当t=
;(3)当t=![]() 时,
时, ![]() ;(4)t=
;(4)t=![]() 时,
时,![]() =
=![]()
【解析】
(1)若DE⊥AC,则∠EDA=90°,易证△ADE∽△ABC,进而列出关于t的比例式,即可求解;
(2)由△CDF∽△CAB,得CF=![]() ,BF=8﹣
,BF=8﹣![]() ,进而用割补法得到
,进而用割补法得到![]() 与
与![]() 之间的关系式,进而即可得到答案;
之间的关系式,进而即可得到答案;
(3)根据![]() ,列出关于t的方程,即可求解;
,列出关于t的方程,即可求解;
(4)过点E作EM⊥AC于点M,易证△AEM∽△ACB,从而得EM=![]() ,AM=
,AM=![]() ,进而得DM=
,进而得DM=![]() ,根据当DM=ME时,
,根据当DM=ME时,![]() =
=![]() ,列出关于t的方程,即可求解.
,列出关于t的方程,即可求解.
(1)∵∠B=![]() ,AB=6 cm,BC=8 cm,
,AB=6 cm,BC=8 cm,
∴AC=10cm,
若DE⊥AC,则∠EDA=90°,
∴∠EDA=∠B,
∵∠A=∠A,
∴△ADE∽△ABC,
∴![]() ,即
,即![]() ,
,
∴t=![]() ,
,
答:当t=![]() 时,DE⊥AC;
时,DE⊥AC;
(2)∵DF⊥BC,
∴∠DFC=90°,
∴∠DFC =∠B,
∵∠C=∠C,
∴△CDF∽△CAB,
∴![]() , 即
, 即![]() ,
,
∴CF=![]() ,
,
∴BF=8﹣![]() ,
,
∴![]() ;
;
(3)若存在某一时刻t,使得![]() ,
,
根据题意得:![]() ,
,
解得:![]() ,
,
答:当t=![]() 时,
时,![]() ;
;
(4)过点E作EM⊥AC于点M,则△AEM∽△ACB
∴![]() =
=![]() ,
,
∴![]() ,
,
∴EM=![]() ,AM=
,AM=![]() ,
,
∴DM=10-2t-![]() =
=![]() ,
,
在Rt△DEM中,当DM=ME时,![]() =
=![]() ,
,
∴![]() ,解得:t=
,解得:t=![]()
即:当t=![]() 时,
时,![]() =
=![]() .
.


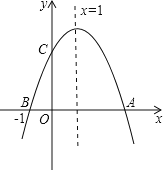
【题目】抛物线y=ax2+bx+c(a≠0,a、b、c为常数)上部分点的横坐标x,纵坐标y的对应值如下表:
x | …… | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | …… |
y | …… |
| 4 |
| 4 | m | 0 | …… |
则下列结论中:①抛物线的对称轴为直线x=﹣1;②m=![]() ;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
A.1个B.2个C.3个D.4个
【题目】为增强中学生体质,篮球运球已列为铜陵市体育中考选考项目,某校学生不仅练习运球,还练习了投篮,下表是一名同学在罚球线上投篮的试验结果,根据表中数据,回答问题.
投篮次数(n) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
投中次数(m) | 28 | 60 | 78 | 104 | 124 | 153 | 252 |
(1)估计这名同学投篮一次,投中的概率约是多少?(精确到0.1)
(2)根据此概率,估计这名同学投篮622次,投中的次数约是多少?