题目内容
【题目】如图,边长为4正方形ABCD中,E为边AD的中点,连接线段EC交BD于点F,点M是线段CE延长线上的一点,且∠MAF为直角,则DM的长为_____.
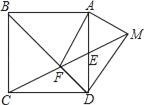
【答案】![]()
【解析】
作MN⊥AD,先证明MA=ME,进而求出AN=NE=1,利用MN∥CD得![]() ,求出MN,在Rt△MND中利用勾股定理即可求出DM.
,求出MN,在Rt△MND中利用勾股定理即可求出DM.
作MN⊥AD垂足为N,
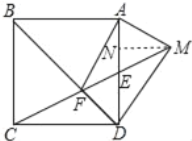
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABF=∠CBF,BC∥AD,∠BAD=∠CDA=90°,
∵BF=BF,
∴△BFA≌△BFC,
∴∠BAF=∠BCF=∠CED=∠AEM,
∵∠MAF=∠BAD=90°,
∴∠BAF=∠MAE,
∴∠MAE=∠AEM,
∴MA=ME,
∵AE=ED=![]() AD=2,
AD=2,
∴![]() ,
,
∵∠MNE=∠CDE=90°,
∴MN∥CD,
∴![]() ,
,
∵CD=4,
∴MN=2,
在Rt△MND中,
∵MN=2,DN=3,
∴![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某班共30名同学参加了网络上第二课堂的禁毒知识竞赛(共20道选择题),学习委员对竞赛结果进行了统计,发现每个人答题正确题数都超过15题.通过统计制成了下表,结合表中信息,解答下列问题:
答对题数 | 16 | 17 | 18 | 19 | 20 |
人数 | 3 | 9 | 6 | 4 |
(1)补统计表中数据:
(2)求这30名同学答对题目的平均数、众数和中位数;
(3)答题正确率为100%的4名同学中恰好是2名男同学和2名女同学,现从中随机抽取2名同学参加学校禁毒知识抢答大赛,问抽到1男1女的概率是多少?