题目内容
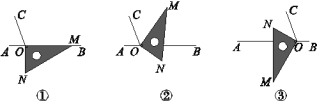
【题目】如图①，O为直线AB上一点，过点O作射线OC，使∠BOC＝110°.将一三角尺的直角顶点放在点O处(∠OMN＝30°)，一边OM在射线OB上，另一边ON在直线AB的下方．
(1)将图①中的三角尺绕点O逆时针旋转至图②，使一边OM在∠BOC的内部，且恰好平分∠BOC，求∠BON的度数；
(2)将图①中的三角尺绕点O以每秒5°的速度按逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，则t的值为________(直接写出结果)；
(3)将图①中的三角尺绕点O顺时针旋转至图③，使ON在∠AOC的内部，请探究∠AOM与∠NOC的数量关系，并说明理由．
【答案】(1) 35°;(2) 11或47;(3)见解析.
【解析】
（1）根据角平分线的定义以及直角的定义，即可求得∠BON的度数；
（2）分两种情况：ON的反向延长线平分∠AOC或射线ON平分∠AOC，分别根据角平分线的定义以及角的和差关系进行计算即可；
（3）根据∠MON=90°，∠AOC=70°，分别求得∠AOM=90°-∠AON，∠NOC=70°-∠AON，再根据∠AOM-∠NOC=（90°-∠AON）-（70°-∠AON）进行计算，即可得出∠AOM与∠NOC的数量关系．
（1）如图2，
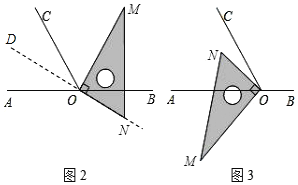
∵OM平分∠BOC，
∴∠MOC=∠MOB，
又∵∠BOC=110°，
∴∠MOB=55°，
∵∠MON=90°，
∴∠BON=∠MON-∠MOB=35°；
（2）分两种情况：
①如图2，∵∠BOC=110°
∴∠AOC=70°，
当直线ON恰好平分锐角∠AOC时，∠AOD=∠COD=35°，
∴∠BON=35°，∠BOM=55°，
即逆时针旋转的角度为55°，
由题意得，5t=55°
解得t=11（s）；
②如图3，当NO平分∠AOC时，∠NOA=35°，
∴∠AOM=55°，
即逆时针旋转的角度为：180°+55°=235°，
由题意得，5t=235°，
解得t=47（s），
综上所述，t=11s或47s时，直线ON恰好平分锐角∠AOC；
故答案为：11或47；
（3）∠AOM-∠NOC=20°．
理由：∵∠MON=90°，∠AOC=70°，
∴∠AOM=90°-∠AON，∠NOC=70°-∠AON，
∴∠AOM-∠NOC=（90°-∠AON）-（70°-∠AON）=20°，
∴∠AOM与∠NOC的数量关系为：∠AOM-∠NOC=20°．
