题目内容
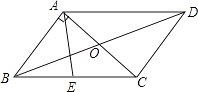
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO,已知BD=![]() .
.
(1)求正方形ABCD的边长;
(2)求OE的长;
(3)①求证:CN=AF;
②直接写出四边形AFBO的面积.

【答案】(1)2;(2)![]() ;(3)①证明见解析,②
;(3)①证明见解析,②![]()
【解析】试题分析:(1)根据正方形的性质以及勾股定理即可求得;(2)根据等腰三角形三线合一的性质证得点E是AF中点,依据三角形中位线OE=![]() CF=
CF=![]() ;(3) ①通过证明△NCB≌△FAB可证得CN=AF; ②依据△AFC的面积-△BOC的面积.
;(3) ①通过证明△NCB≌△FAB可证得CN=AF; ②依据△AFC的面积-△BOC的面积.
试题解析:
(1)∵四边形ABCD是正方形,
∴AB=CD=BC,∠BCD=∠ABC=90°,
∴2BC2=BD2,∵BD=![]() ,∴AB= BC =2,
,∴AB= BC =2,
∴正方形ABCD的边长为2;
(2)∵CF=CA,AF是∠ACF的平分线,
∴CE⊥AF,∴∠AEC=∠CEF=90°,E为AF的中点,
∵正方形ABCD,∴O为AC的中点,AC=BD=![]() ,
,
∴OE=![]() CF=
CF=![]() BD=
BD=![]() ,
,
(3)①证明:∵∠ABC=∠ABF=∠CEF=90°,AB=BC,
∴∠ECB+∠F=∠FAB+∠F=90°,∴∠ECB=∠FAB,
∴△NCB≌△FAB,
∴CN=AF.
②![]() .
.
点睛:本题综合考查了菱形、矩形、正方形的有关性质及判定,其中还串联到等腰三角形和勾股定理等知识,充分体现出几何知识的整体性和推理的严密性.在解答有关特殊四边形的性质或判定问题时,既要依托数,也要依托形,这是解答几何问题的最基本的思想方法.

练习册系列答案
相关题目