题目内容
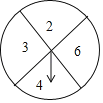
【题目】如图是一个转盘,转盘被平均分成4等分,即被分成4个大小相等的扇形,4个扇形分别标有数字2、3、4、6,指针的位置固定,转动转盘后任其自由停止,每次指针落在每个扇形的机会均等(若指针恰好落在分界线上则重转).
(1)若图中标有“2”的扇形至少绕圆心旋转n度能与标有“3”的扇形的起始位置重合,求n的值;
(2)现有一张电影票,兄弟俩商定通过转盘游戏定输赢(赢的一方先得).游戏规则是:姐妹俩各转动一次转盘,两次转动后,若指针所指扇形上的数字之和为小于8,则哥哥赢;若指针所指扇形上的数字之和不小于8,则弟弟赢.这个游戏规则对双方公平吗?请利用树状图或列表法说明理由.
【答案】(1)n=90°;(2)公平,理由见解析.
【解析】
(1)根据题意求出每份的圆心角的度数,再根据(2)与(3)的位置,即可得出答案;
(2)根据题意列出图表,再根据概率公式求出指针所指扇形上的数字之和小于8的概率和指针所指扇形上的数字之和不小于8的概率,然后进行比较,即可得出答案.
解:(1)∵转盘被平均分成4等份,
∴n=360°÷4=90°;
(2)公平,
列表如下:
a b | 2 | 3 | 4 | 6 |
2 | 4 | 5 | 6 | 8 |
3 | 5 | 6 | 7 | 9 |
4 | 6 | 7 | 8 | 10 |
6 | 8 | 9 | 10 | 12 |
由表可知,共有16种等可能结果,其中数字之和为小于8的有8种结果,数字之和不小于8的也有8种结果,所以这个游戏规则公平.

练习册系列答案
相关题目