题目内容
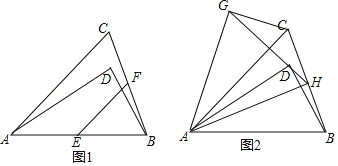
【题目】如图,在三角形ABC中,AB=AC,点D在△ABC内,且∠ADB=90°.
(1)如图1,若∠BAD=30°,AD=3![]() ,点E、F分别为AB、BC边的中点,连接EF,求线段EF的长;
,点E、F分别为AB、BC边的中点,连接EF,求线段EF的长;
(2)如图2,若△ABD绕顶点A逆时针旋转一定角度后能与△ACG重合,连接GD并延长交BC于点H,连接AH,求证:∠DAH=∠DBH.
【答案】(1)EF =3;(2)证明见解析.
【解析】
(1) 设BD=x,则AB=2x,由勾股定理得:![]() ,求出AB,再根据中位线性质求出EF;
,求出AB,再根据中位线性质求出EF;
(2) 在GH上取一点M,使GM=DH,由性质性质得△ADB≌△AGC,再证△CGM≌△BDH,得CM=BH,∠GCM=∠DBH,因为∠CMH=∠MGC+∠MCG,∠CHM=∠BDH+∠DBH,
所以∠CMH=∠CHM,可得CM=CH=BH,又AC=AB,所以AH⊥BC,∠AHB=90°=∠ADB,
又∠AOD=∠BOH,故∠DAH=∠DBH.
(1)解:如图1,在Rt△ABD中,∠BAD=30°,
∴AB=2BD,
设BD=x,则AB=2x,
由勾股定理得:![]() ,
,
x=3或﹣3(舍),
∴AB=2x=6,
∵AC=AB=6,
∵点E、F分别为AB、BC边的中点,
∴EF=![]() AC=3;
AC=3;
(2)证明:如图2,由旋转得:△ADB≌△AGC,
∴AG=AD,∠AGC=∠ADB=90°,CG=BD,
∴∠AGD=∠ADG,
∵∠ADB=90°,
∴∠ADG+∠BDH=90°,
∵∠AGD+∠MGC=90°,
∴∠MGC=∠BDH,
在GH上取一点M,使GM=DH,
∴△CGM≌△BDH,
∴CM=BH,∠GCM=∠DBH,
∵∠CMH=∠MGC+∠MCG,∠CHM=∠BDH+∠DBH,
∴∠CMH=∠CHM,
∴CM=CH=BH,
∵AC=AB,
∴AH⊥BC,即∠AHB=90°=∠ADB,
∵∠AOD=∠BOH,
∴∠DAH=∠DBH.