ЬтФПФкШн
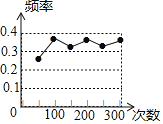
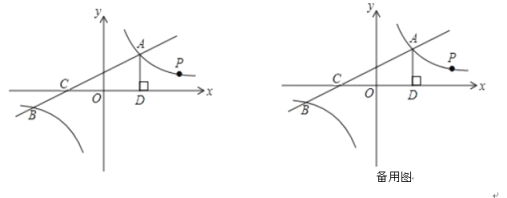
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y1ЃНk1x+2гыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЕуAЃЈ4ЃЌmЃЉКЭBЃЈЉ8ЃЌЉ2ЃЉгыxжсНЛгкЕуCЃЎЙ§ЕуAзїADЁЭxжсгкЕуD
ЕФЭМЯѓНЛгкЕуAЃЈ4ЃЌmЃЉКЭBЃЈЉ8ЃЌЉ2ЃЉгыxжсНЛгкЕуCЃЎЙ§ЕуAзїADЁЭxжсгкЕуD
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФНтЮіЪНЃЎ
ЃЈ2ЃЉИљОнКЏЪ§ЭМЯѓжЊЃЌЕБy1ЃОy2ЪБЃЌxЕФШЁжЕЗЖЮЇЪЧ ЃЛ
ЃЈ3ЃЉСЌНгBDЃЌЧѓЁїABDЕФУцЛ§
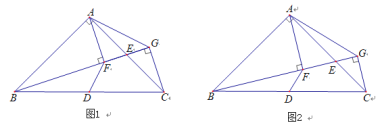
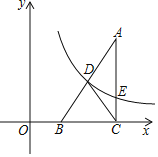
ЃЈ4ЃЉЕуPЪЧЗДБШР§КЏЪ§дкЕквЛЯѓЯоЕФЭМЯѓЩЯвЛЕуЃЌЩшжБЯпOPгыЯпЖЮADНЛгкЕуEЃЌЕБЁїODEЁзЁїCDAЪБЃЌЧѓЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛ
ЃЛ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() Лђ
Лђ![]() ЃЛЃЈ3ЃЉ24ЃЛЃЈ4ЃЉ
ЃЛЃЈ3ЃЉ24ЃЛЃЈ4ЃЉ![]()
ЁОНтЮіЁП
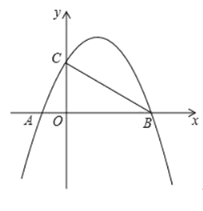
ЃЈ1ЃЉЗжБ№АбЕуBДњШывЛДЮКЏЪ§ЕФНтЮіЪНКЭЗДБШР§КЏЪ§ЕФНтЮіЪНЃЌМДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉНсКЯЕуAЁЂBЕФКсзјБъЃЌвЛДЮКЏЪ§ЭМЯёдкЗДБШР§КЏЪ§ЭМЯёЕФЩЯЗНЃЌМДПЩЕУЕНД№АИЃЛ
ЃЈ3ЃЉзї![]() гк
гк![]() ЃЌЯШЧѓГіЕуAЕФзјБъЃЌШЛКѓЧѓГіADКЭBEЕФГЄЖШЃЌМДПЩЕУЕНД№АИЃЛ
ЃЌЯШЧѓГіЕуAЕФзјБъЃЌШЛКѓЧѓГіADКЭBEЕФГЄЖШЃЌМДПЩЕУЕНД№АИЃЛ
ЃЈ4ЃЉгЩЯрЫЦШ§НЧаЮЕФаджЪЃЌЕУЕН![]() ЃЌШЛКѓЕУЕНжБЯпOPЕФНтЮіЪНЃЌНсКЯЗДБШР§КЏЪ§ЕФНтЮіЪНЃЌМДПЩЧѓГіЕуPЕФзјБъ.
ЃЌШЛКѓЕУЕНжБЯпOPЕФНтЮіЪНЃЌНсКЯЗДБШР§КЏЪ§ЕФНтЮіЪНЃЌМДПЩЧѓГіЕуPЕФзјБъ.
НтЃКЃЈ1ЃЉНЋЕу![]() ДњШы
ДњШы![]() ЃЌдђ
ЃЌдђ
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЛ
ЃЛ
Ёр![]()
НЋЕу![]() ДњШы
ДњШы![]() ЃЌдђ
ЃЌдђ
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЎ
ЃЎ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпвЛДЮКЏЪ§y1=k1x+2гыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЕуAЃЈ4ЃЌmЃЉКЭBЃЈ-8ЃЌ-2ЃЉЃЌ
ЕФЭМЯѓНЛгкЕуAЃЈ4ЃЌmЃЉКЭBЃЈ-8ЃЌ-2ЃЉЃЌ
ЁрЕБy1ЃОy2ЪБЃЌxЕФШЁжЕЗЖЮЇЪЧЃК![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃК![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМЃКСЌНгBDЃЌзї![]() гк
гк![]() ЃЌ
ЃЌ

Абx=4ДњШы![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
ЃЈ4ЃЉШчЭМЃК
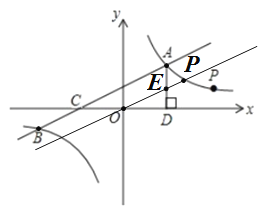
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЕФНтЮіЪНЮЊЃК
ЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
гжЁпжБЯпOPОЙ§дЕуOЃЌ
ЁржБЯп![]() ЕФНтЮіЪНЮЊЃК
ЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
СЊСЂжБЯп![]() гыЗДБШР§КЏЪ§НтЮіЪНзщГЩЗНГЬзщЃЌ
гыЗДБШР§КЏЪ§НтЮіЪНзщГЩЗНГЬзщЃЌ
Ёр ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() .
.

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ