Question

【题目】阅读下列材料，完成（1）~（3）题：

数学课上，老师出示了这样一道题：

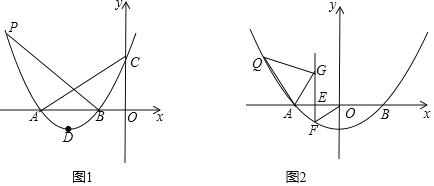
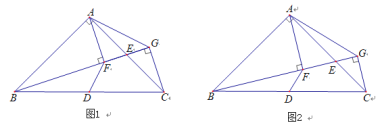
如图1，△ABC中，AB=AC，∠BAC=90°，点D是BC的中点，E是AC的中点，经过点A、C作射线BE的垂线，垂足分别为点F、G，连接AG．探究线段DF和AG的关系．某学习小组的同学经过思考后，交流了自己的想法：

小明：“经过观察和度量，发现∠ABF和∠ACG相等．”小刚：“经过观察和度量，发现有两条线段和AF相等．”

小伟：“通过构造全等三角形，经过进一步推理，可以得到线段DF和AG的关系．”

……

老师：“若点E不是AC的中点，其他条件不变（如图2），可以求出的值．”

（1）求证：AF=FG；

（2）探究线段DF和AG的关系，并证明；

（3）直接写出的值．

Answer 1

【答案】（1）证明见解析；（2），证明见解析；（3）．

【解析】

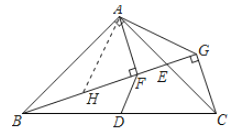
（1）如图1中，作AH⊥AG交BG于H．证明△ABH≌△ACG（ASA）可得结论．

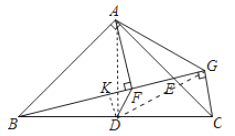
（2）结论：AG=2DF，DF⊥AG．如图2中，连接AD，DG，作DK⊥BG于K．证明△DFA≌△DFG（SSS），推出∠ADF=∠GDF，可得DF⊥AG，再证明DF=DK，AG=AF，AF=CG=2DK即可解决问题．

（3）利用（2）中结论即可解决问题．

（1）证明：过点作，交于．

∴．

∵，

∴．

∵，

∴．

又∵，，

∴．

∵，

∴．

∴．

∵，

∴．

∴．

（2）证明：作．如图：

∵，，

∴．

∵，，

∴．

∴．

∴．

∵，

∴．

∵，

∴．

∵，，，

∴．

∴．

∵，

∴．

∴．

∴．

∴．

∴．

又∵，

∴．

（3）由（2）可知：CG=2DK，DF=DK，
∴．