题目内容
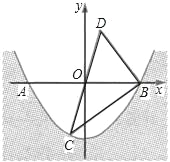
【题目】如图,△ABC的边BC在x轴上,且∠ACB=90°.反比例函数y=![]() (x>0)的图象经过AB边的中点D,且与AC边相交于点E,连接CD.已知BC=2OB,△BCD的面积为6.
(x>0)的图象经过AB边的中点D,且与AC边相交于点E,连接CD.已知BC=2OB,△BCD的面积为6.
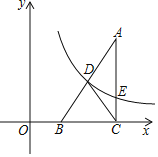
(1)求k的值;(2)若AE=BC,求点A的坐标.
【答案】(1)k=12;(2)A(6,6).
【解析】
(1)连接OD,过D作DF⊥OC于F,依据∠ACB=90°,D为AB的中点,即可得到CD=![]() AB=BD,进而得出BC=2BF=2CF,依据BC=2OB,即可得到OB=BF=CF,进而得出k=xy=OFDF=BCDF=2S△BCD=12;
AB=BD,进而得出BC=2BF=2CF,依据BC=2OB,即可得到OB=BF=CF,进而得出k=xy=OFDF=BCDF=2S△BCD=12;
(2)设OB=m,则OF=2m,OC=3m,DF=![]() ,进而得到E(3m,
,进而得到E(3m,![]() -2m),依据3m(
-2m),依据3m(![]() -2m)=12,即可得到m=2,进而得到A(6,6).
-2m)=12,即可得到m=2,进而得到A(6,6).
解:(1)如图,连接OD,过D作DF⊥OC于F,
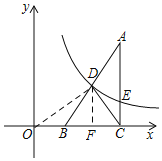
∵∠ACB=90°,D为AB的中点,
∴CD=![]() AB=BD,
AB=BD,
∴BC=2BF=2CF,
∵BC=2OB,
∴OB=BF=CF,
∴k=xy=OFDF=BCDF=2S△BCD=12;
(2)设OB=m,则OF=2m,OC=3m,DF=![]() ,
,
∵DF是△ABC的中位线,
∴AC=2DF=![]() ,
,
又∵AE=BC=2m,
∴CE=AC-AE=![]() -2m,
-2m,
∴E(3m,![]() -2m),
-2m),
∵3m(![]() -2m)=12,
-2m)=12,
∴m2=4,
又∵m>0,
∴m=2,
∴OC=6,AC=6,
∴A(6,6).

 习题精选系列答案
习题精选系列答案【题目】某商场销售![]() 、
、![]() 两种品牌的洗衣机,进价及售价如下表:
两种品牌的洗衣机,进价及售价如下表:
品牌 |
|
|
进价(元/台) | 1500 | 1800 |
售价(元/台) | 1800 | 2200 |
(1)该商场9月份用45000元购进![]() 、
、![]() 两种品牌的洗衣机,全部售完后获利9600元,求商场9月份购进
两种品牌的洗衣机,全部售完后获利9600元,求商场9月份购进![]() 、
、![]() 两种洗衣机的数量;
两种洗衣机的数量;
(2)该商场10月份又购进![]() 、
、![]() 两种品牌的洗衣机共用去36000元
两种品牌的洗衣机共用去36000元
①问该商场共有几种进货方案?请你把所有方案列出来;
②通过计算说明洗衣机全部销售完后哪种进货方案所获得的利润最大