题目内容
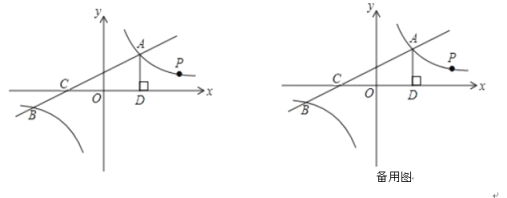
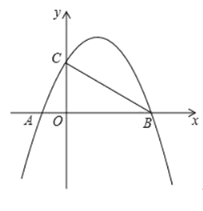
【题目】如图,已知抛物线yax2bxc(a0)经过A(1,0),B(4,0),C(0,2)三点.
(1)求这条抛物线和直线BC的解析式;
(2)E为抛物线上一动点,是否存在点E,使以A、B、E为顶点的三角形与COB相似?若存在,试求出点E的坐标;若不存在,请说明理由
【答案】(1)![]() ;
;![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)设抛物线的解析式为![]() ,把点C的坐标代入求出a的值即可得出抛物线的解析式;然后利用待定系数法求直线BC的解析式;
,把点C的坐标代入求出a的值即可得出抛物线的解析式;然后利用待定系数法求直线BC的解析式;
(2)易得![]() 只能是以E为直角顶点的三角形,利用勾股定理的逆定理可证明
只能是以E为直角顶点的三角形,利用勾股定理的逆定理可证明![]() ,再证明
,再证明![]() ,所以当点E在点C时满足条件,当E为点C在抛物线上的对称点时也满足条件,利用对称性写出点E的坐标即可.
,所以当点E在点C时满足条件,当E为点C在抛物线上的对称点时也满足条件,利用对称性写出点E的坐标即可.
解:(1)设抛物线解析式为![]() ,
,
把![]() 代入得
代入得![]() ,
,
解得:![]() ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ,
,
即![]() ;
;
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入,
代入,
得![]() ,
,
解得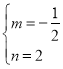 ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ;
;
(2)存在.
由图象可得以![]() 或
或![]() 点为直角顶点的
点为直角顶点的![]() 不存在,
不存在,

![]() 只能是以
只能是以![]() 点为直角顶点的三角形,
点为直角顶点的三角形,
![]()
![]() ,
,
![]() ,
,
![]() 为直角三角形,
为直角三角形,![]() ,
,
![]() ,
,
![]()
![]() 当点
当点![]() 在点
在点![]() 时,以
时,以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似;
相似;
![]() 点
点![]() 关于直线
关于直线![]() 的对称点的坐标为
的对称点的坐标为![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() 时,以
时,以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,
相似,
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目