ЬтФПФкШн
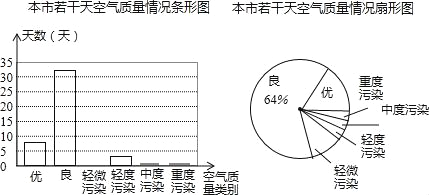
ЁОЬтФПЁПЮЊТфЪЕЁАУРРіЬЉжнЁБЕФЙЄзїВПЪ№ЃЌЪаеўИЎМЦЛЎЖдГЧЧјЕРТЗНјааИФдьЃЌЯжАВХХМзЁЂввСНИіЙЄГЬЖгЭъГЩИУИФдьЙЄзї.вбжЊМзЖгЕФЙЄзїаЇТЪЪЧввЖгЙЄзїаЇТЪЕФ![]() БЖЃЌМзЖгИФдь720УзЕФЕРТЗБШввЖгИФдьЭЌбљГЄЕФЕРТЗЩйгУ4Ьь.
БЖЃЌМзЖгИФдь720УзЕФЕРТЗБШввЖгИФдьЭЌбљГЄЕФЕРТЗЩйгУ4Ьь.
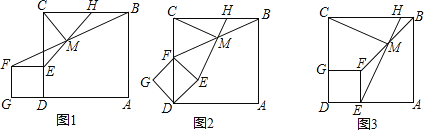
(1)МзЁЂввСНЙЄГЬЖгУПЬьФмИФдьЕРТЗЕФГЄЖШЗжБ№ЪЧЖрЩйУзЃП
(2)ШєМзЖгЙЄзївЛЬьашИЖЗбгУ7ЭђдЊЃЌввЖгЙЄзївЛЬьашИЖЗбгУ5ЭђдЊЃЌШєашИФдьЕФЕРТЗШЋГЄ2400УзЃЌИФдьзмЗбгУВЛГЌЙ§195ЭђдЊЃЌдђжСЩйАВХХМзЖгЙЄзїЖрЩйЬьЃП
ЁОД№АИЁП(1)МзЁЂввСНЙЄГЬЖгУПЬьФмИФдьЕРТЗЕФГЄЖШЗжБ№90УзЃЌ60УзЃЛ(2)жСЩйАВХХМзЖгЙЄзї10Ьь.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнМзЖгИФдь720УзЕФЕРТЗБШввЖгИФдьЭЌбљГЄЕФЕРТЗЩйгУ4ЬьРДСаГіЗНГЬЃЌНтЗНГЬМДПЩЃЛЃЈ2ЃЉЩшжСЩйАВХХМзЖгЙЄзїmЬьЃЌИљОнЁАИФдьзмЗбгУВЛГЌЙ§195ЭђдЊЁБСаГіВЛЕШЪНЃЌНтВЛЕШЪНМДПЩ
(1)ЩшввxЃЌМз![]()
ПЩЕУГі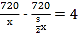
ЧѓГіx=60ЃЌОМьбщx=60ЪЧдЗНГЬЕФНт
МзЮЊ90ЃЌввЮЊ60
(2)ЩшжСЩйАВХХМзЖгЙЄзїmЬьЃЌвв![]()
![]()
mЁн10
Д№ЃКжСЩйАВХХМз10Ьь.

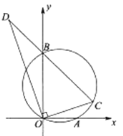
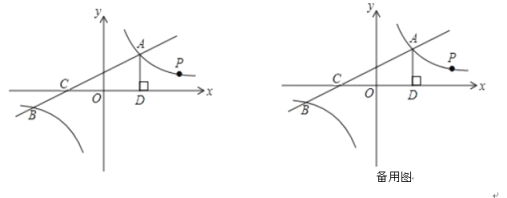
ЁОЬтФПЁПЃЈЬНОПгыДДаТЃЉЃКвбжЊAЁЂBдкЪ§жсЩЯЗжБ№БэЪОaЁЂb
ЂйЖдееЪ§жсЬюаДЯТБэЃК
a | 6 | Љ6 | Љ6 | 2 | Љ1.5 |
b | 4 | 0 | Љ4 | Љ10 | Љ1.5 |
AЁЂBСНЕуЕФОрРы | 2 | ЁЁ ЁЁ | ЁЁ ЁЁ | ЁЁ ЁЁ | 0 |
ЂкШєAЁЂBСНЕуМфЕФОрРыМЧЮЊdЃЌдђdКЭaЁЂbжЎМфгаКЮЪ§СПЙиЯЕЃПЃЈжБНгаДГіНсЙћЃЉ
ЂлдкЪ§жсЩЯБъГіЫљгаЗћКЯЬѕМўЕФећЪ§ЕуPЪЙЫќЕН5КЭЉ5ЕФОрРыжЎКЭЮЊ10ЃЌВЂЧѓГіЫљгаетаЉећЪ§ЕФКЭЃЎ
![]()
ЂмШєЕуQБэЪОЕФЪ§ЮЊxЃЌЕБЕуQдкЪВУДЮЛжУЪБЃЌ|x+1|+|xЉ2|газюаЁжЕЃПзюаЁжЕЪЧЖрЩйЃП