题目内容
【题目】如图,矩形ABCD的对角线AC.BD相交于点O , 过点O作OE⊥AC交AD于E , 若AB=6,AD=8,求sin∠OEA的值 . 
【答案】解:连接EC , 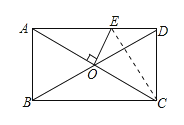
∵四边形ABCD为矩形,
∴OA=OC , ∠ABC=90°,
利用勾股定理得:AC= ![]() =10,即OA=5,
=10,即OA=5,
∵OE⊥AC ,
∴AE=CE ,
在Rt△EDC中,设EC=AE=x , 则有ED=AD-AE=8-x , DC=AB=6,
根据勾股定理得:x2=(8-x)2+62,
解得:x= ![]() ,
,
∴AE= ![]() ,
,
在Rt△AOE中,sin∠OEA= ![]() .
.
【解析】连接EC , 由四边形ABCD为矩形,得到对角线互相平分,即O为AC中点,再由OE垂直AC , 得到OE垂直平分AC , 即AE=CE , 在直角三角形EDC中,设EC=AE=x , 利用勾股定理列出关于x的方程,求出方程的解得到EC的长,即为AE的长,利用勾股定理求出AC的长,进而求出OA的长,在直角三角形AOE中,利用锐角三角函数定义即可求出sin∠OEA的值 .
【考点精析】通过灵活运用解直角三角形,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.

练习册系列答案
相关题目