Question

【题目】如图，斜面AC的坡度（CD与AD的比）为1：2，AC=3 米，坡顶有旗杆BC ， 旗杆顶端B点与A点有一条彩带相连 ． 若AB=10米，则旗杆BC的高度为（　　）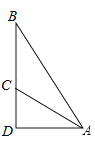

A.5米
B.6米
C.8米
D.（3+ ）米

Answer 1

【答案】A
【解析】设CD=x ， 则AD=2x ，
由勾股定理可得，AC=
∵AC=3 米，
∴ x=3 ，
∴x=3米，
∴CD=3米，
∴AD=2×3=6米，
在Rt△ABD中，BD= =8米，
∴BC=8-3=5米 ．
故选A.
【考点精析】解答此题的关键在于理解关于坡度坡角问题的相关知识，掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)．用字母i表示，即i=h/l．把坡面与水平面的夹角记作A(叫做坡角)，那么i=h/l=tanA．