ĢāÄæÄŚČŻ
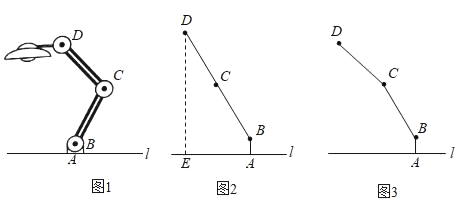
”¾ĢāÄæ”æČēĶ¼1£¬µćOŌŚĻ߶ĪABÉĻ£¬AO£½4£¬OB£½2£¬OCĪŖÉäĻߣ¬ĒŅ”ĻBOC£½60”ć£¬¶ÆµćPŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶Č“ÓµćO³ö·¢£¬ŃŲÉäĻßOC×öŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£®
£Ø1£©µ±t£½1ĆėŹ±£¬ŌņOP£½”” ””£¬S”÷ABP£½”” ””£»
£Ø2£©µ±”÷ABPŹĒÖ±½ĒČż½ĒŠĪŹ±£¬ĒótµÄÖµ£»
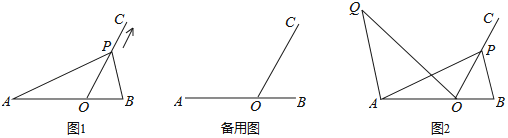
£Ø3£©ČēĶ¼2£¬µ±AP£½ABŹ±£¬¹żµćA×÷AQ”ĪBP£¬²¢Ź¹µĆ”ĻQOP£½”ĻB£¬ĒóAQBPµÄÖµ£®ĪŖĮĖĒóAQBPµÄÖµ£¬Š”»ŖĶ¬Ń§³¢ŹŌ¹żOµć×÷OE”ĪAP½»BPÓŚµćE£¬ŹŌĄūÓĆŠ”»ŖĶ¬Ń§øųĪŅĆĒµÄĘō·¢²¹Č«Ķ¼ŠĪ²¢ĒóAQBPµÄÖµ£®
”¾“š°ø”æ£Ø1£©2£¬3![]() £»£Ø2£©µ±”÷ABPŹĒÖ±½ĒČż½ĒŠĪŹ±£¬t£½2»ņt£½
£»£Ø2£©µ±”÷ABPŹĒÖ±½ĒČż½ĒŠĪŹ±£¬t£½2»ņt£½![]() £»£Ø3£©²¹Č«Ķ¼ŠĪ¼ū½āĪö£¬AQPB£½12£®
£»£Ø3£©²¹Č«Ķ¼ŠĪ¼ū½āĪö£¬AQPB£½12£®
”¾½āĪö”æ
£Ø1£©×÷PD”ĶABÓŚµćD£¬ĄūÓĆČż½ĒŗÆŹżĒó½ā£»
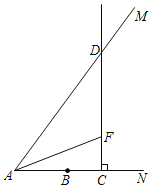
£Ø2£©µ±”÷ABPŹĒÖ±½ĒČż½ĒŠĪŹ±£¬·Ö”ĻA£½90”ć”¢”ĻB£½90”ć”¢”ĻAPB£½90”ć£¬»³ö¶ŌÓ¦Ķ¼ŠĪ£¬ĄūÓĆ30”ć½ĒĖł¶ŌµÄÖ±½Ē±ßµČÓŚŠ±±ßµÄŅ»°ė¼°¹“¹É¶ØĄķĒó½ā£»
£Ø3£©¹żµćO×÷OE”ĪAP£¬½»PBÓŚµćE£¬¹¹ŌģŅ»¶ŌĻąĖĘČż½ĒŠĪ£¬¼“”÷OAQ”×”÷PEO£¬ĄūÓƶŌÓ¦±ß³É±ČĄżĒó½ā.
£Ø1£©µ±t£½1ĆėŹ±£¬OP£½2t£½2”Į1£½2£®
Čē“šĶ¼1£¬¹żµćP×÷PD”ĶABÓŚµćD£®
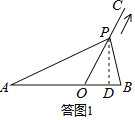
ŌŚRt”÷PODÖŠ£¬PD£½OPsin60”ć£½2”Į![]() £½
£½![]() £¬
£¬
”ąS”÷ABP£½![]() ABPD£½
ABPD£½![]() ”Į£Ø4+2£©”Į
”Į£Ø4+2£©”Į![]() £½3
£½3![]() £®
£®
¹Ź“š°øĪŖ£ŗ2£¬3![]() £®
£®
£Ø2£©µ±”÷ABPŹĒÖ±½ĒČż½ĒŠĪŹ±£¬
¢ŁČō”ĻA£½90”ć£®
”ß”ĻBOC£½60”ćĒŅ”ĻBOC£¾”ĻA£¬
”ą”ĻA”Ł90”ć£¬¹Ź“ĖÖÖĒéŠĪ²»“ęŌŚ£»
¢ŚČō”ĻB£½90”ć£¬Čē“šĶ¼2ĖłŹ¾£ŗ
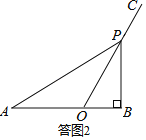
”ß”ĻBOC£½60”ć£¬
”ą”ĻBPO£½30”ć£¬
”ąOP£½2OB£½4£¬ÓÖOP£½2t£¬
”ąt£½2£»
¢ŪČō”ĻAPB£½90”ć£¬Čē“šĶ¼3ĖłŹ¾£ŗ
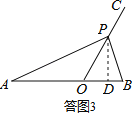
¹żµćP×÷PD”ĶABÓŚµćD£¬ŌņOD£½OPsin30”ć£½t£¬PD£½OPsin60”ć£½![]() t£¬
t£¬
”ąAD£½OA+OD£½4+t£¬BD£½OB-OD£½2-t£®
ŌŚRt”÷ABPÖŠ£¬Óɹ“¹É¶ØĄķµĆ£ŗPA2+PB2£½AB2
”ą£ØAD2+PD2£©+£ØBD2+PD2£©£½AB2£¬
¼“[£Ø4+t£©2+£Ø![]() t£©
t£©![]() t£©2]£½62£¬
t£©2]£½62£¬
½ā·½³ĢµĆ£ŗt£½![]() »ņt£½
»ņt£½![]() £ØøŗÖµÉįČ„£©£¬
£ØøŗÖµÉįČ„£©£¬
”ąt£½![]() £®
£®
×ŪÉĻĖłŹö£¬µ±”÷ABPŹĒÖ±½ĒČż½ĒŠĪŹ±£¬t£½2»ņt£½![]() £®
£®
£Ø3£©Čē“šĶ¼4£¬¹żµćO×÷OE”ĪAP£¬½»PBÓŚµćE£¬
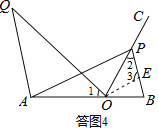
ŌņÓŠ![]() £½
£½![]() £¬
£¬
”ąPE£½![]() PB£®
PB£®
”ßAP£½AB£¬
”ą”ĻAPB£½”ĻB£¬
”ßOE”ĪAP£¬
”ą”ĻOEB£½”ĻAPB£¬
”ą”ĻOEB£½”ĻB£¬
”ąOE£½OB£½2£¬”Ļ3+”ĻB£½180”ć£®
”ßAQ”ĪPB£¬
”ą”ĻOAQ+”ĻB£½180”ć£¬
”ą”ĻOAQ£½”Ļ3£»
”ß”ĻAOP£½”Ļ1+”ĻQOP£½”Ļ2+”ĻB£¬”ĻQOP£½”ĻB£¬
”ą”Ļ1£½”Ļ2£»
”ą”÷OAQ”×”÷PEO£¬
”ą![]() £½£¬¼“
£½£¬¼“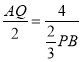 £¬
£¬
»Æ¼ņµĆ£ŗAQPB£½12£®

 »īĮ¦æĪŹ±Ķ¬²½Į·Ļ°²įĻµĮŠ“š°ø
»īĮ¦æĪŹ±Ķ¬²½Į·Ļ°²įĻµĮŠ“š°ø ѧŅµ²āĘĄŅ»æĪŅ»²āĻµĮŠ“š°ø
ѧŅµ²āĘĄŅ»æĪŅ»²āĻµĮŠ“š°ø