题目内容
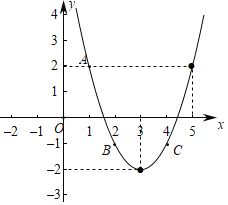
【题目】如图,在平面直角坐标系中,已知某个二次函数的图象经过点A(1,2),B(2,﹣1),C(4,﹣1),且该二次函数的最小值是﹣2.

(1)请在图中描出该函数图象上另外的两个点,并画出图象;
(2)求出该二次函数的解析.
【答案】(1)见解析;(2)y=x2﹣6x+7.
【解析】
(1)根据B、C两点的坐标和函数最小值,可以确定函数的对称轴以及函数的顶点坐标,然后根据抛物线的对称性,找到对称点,连线即可.
(2)已知抛物线的对称轴和顶点坐标,所以设顶点式,然后找到一个点(非顶点坐标)代入求解计算即可.
(1)∵B(2,﹣1),C(4,﹣1),且该二次函数的最小值是﹣2.
∴该二次函数图象的顶点为(3,﹣2),
∵点A(1,2),
∴A关于对称轴对称的点为(5,2),
利用描点法可画出函数图象,如图;
(2)设抛物线的解析式为y=a(x﹣3)2﹣2,
代入A(1,2)得2=4a﹣2,解得a=1,
∴该二次函数的解析式为y=x2﹣6x+7.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目