题目内容
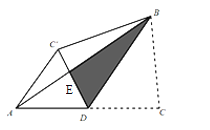
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
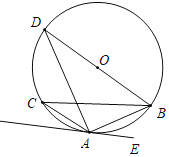
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=8,AB=2![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)见解析;(2)5
【解析】
(1)连接OA,根据圆周角定理、等腰三角形的性质和已知,求出∠DAO=∠BAE,∠DAB=90°,求出OAE=90,根据切线的判定得出即可;
(2)根据垂径定理求出BF,根据勾股定理求出AF,再根据勾股定理求出OB即可.
(1)连接OA交BC于点F,
∵OA=OD,
∴∠D=∠DAO,
∵由圆周角定理得:∠D=∠C,
∴∠C=∠DAO,
又∵∠C=∠BAE,
∴∠DAO=∠BAE,
∵BD为⊙O的直径,
∴∠DAB=∠DAO+∠OAB=90°,
∴∠OAB+∠BAE=90°,即OA⊥AE,
∵OA是半径,
∴AE与⊙O相切于点A;
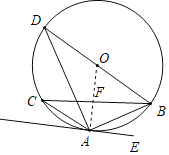
(2)∵AE∥BC,AE⊥OA,
∴OA⊥BC,
∴FB=![]() BC=
BC=![]() ×8=4,
×8=4,
∴在Rt△ABF中,AF=![]() =
=![]() =2,
=2,
∵在Rt△OFB中,OB2=BF2+OF2,
∴OB2=42+(0B﹣2)2,
∴OB=5,
∴⊙O的半径为5.

练习册系列答案
相关题目
【题目】某农科所在相同条件下做某种作物种子发芽率的试验,结果如表所示:
种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
发芽种子频率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
则该作物种子发芽的概率约为_____________.(保留一位小数)