ЬтФПФкШн
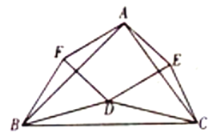
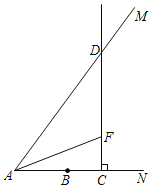
ЁОЬтФПЁПШчЭМЃЌЩфЯпANЩЯгавЛЕуBЃЌABЃН5ЃЌtanЁЯMANЃН![]() ЃЌЕуCДгЕуAГіЗЂвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШбиЩфЯпANдЫЖЏЃЌЙ§ЕуCзїCDЁЭANНЛЩфЯпAMгкЕуDЃЌдкЩфЯпCDЩЯШЁЕуFЃЌЪЙЕУCFЃНCBЃЌСЌНсAFЃЎЩшЕуCЕФдЫЖЏЪБМфЪЧtЃЈУыЃЉЃЈtЃО0ЃЉЃЎ
ЃЌЕуCДгЕуAГіЗЂвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШбиЩфЯпANдЫЖЏЃЌЙ§ЕуCзїCDЁЭANНЛЩфЯпAMгкЕуDЃЌдкЩфЯпCDЩЯШЁЕуFЃЌЪЙЕУCFЃНCBЃЌСЌНсAFЃЎЩшЕуCЕФдЫЖЏЪБМфЪЧtЃЈУыЃЉЃЈtЃО0ЃЉЃЎ
ЃЈ1ЃЉЕБЕуCдкЕуBгвВрЪБЃЌЧѓADЁЂDFЕФГЄЃЎЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉСЌНсBDЃЌЩшЁїBCDЕФУцЛ§ЮЊSЦНЗНЕЅЮЛЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ3ЃЉЕБЁїAFDЪЧжсЖдГЦЭМаЮЪБЃЌжБНгаДГіtЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉADЃН5tЃЌDF=t+5ЃЎЃЈ2ЃЉЕБ0ЃМtЃМ![]() ЪБЃЌSЃНЉ6t2+10tЃЎЕБtЃО
ЪБЃЌSЃНЉ6t2+10tЃЎЕБtЃО![]() ЪБЃЌSЃН6t2Љ10tЃЎЃЈ3ЃЉtЕФжЕЮЊ
ЪБЃЌSЃН6t2Љ10tЃЎЃЈ3ЃЉtЕФжЕЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
(1)РћгУЙДЙЩЖЈРэЫуГіAD,БэЪОГіCB,МДПЩБэЪОГіDF.
(2)ЗжБ№ЬжТл0ЃМtЃМ![]() ЪБКЭtЃО
ЪБКЭtЃО![]() ЪБ,РћгУУцЛ§ЙЋЪНМЦЫуМДПЩ.
ЪБ,РћгУУцЛ§ЙЋЪНМЦЫуМДПЩ.
(3)ЗжБ№ЬжТлЕБDFЃНADЪБЕФвЛжжЧщПіЁЂЕБAFЃНDFЪБЕФСНжжЧщПі.
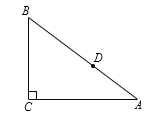
НтЃКЃЈ1ЃЉдкRtЁїACDжаЃЌACЃН3tЃЌtanЁЯMANЃН![]() ЃЌ
ЃЌ
ЁрCDЃН4tЃЎ
ЁрADЃН![]() ЃЌ
ЃЌ
ЕБЕуCдкЕуBгвВрЪБЃЌCBЃН3tЉ5ЃЌ
ЁрCFЃНCBЃЎ
ЁрDFЃН4tЉЃЈ3tЉ5ЃЉЃНt+5ЃЎ
ЃЈ2ЃЉЕБ0ЃМtЃМ![]() ЪБЃЌSЃН
ЪБЃЌSЃН![]() ЃЈ5Љ3tЃЉ4tЃНЉ6t2+10tЃЎ
ЃЈ5Љ3tЃЉ4tЃНЉ6t2+10tЃЎ
ЕБtЃО![]() ЪБЃЌSЃН
ЪБЃЌSЃН![]() ЃЈ3tЉ5ЃЉ4tЃН6t2Љ10tЃЎ
ЃЈ3tЉ5ЃЉ4tЃН6t2Љ10tЃЎ
ЃЈ3ЃЉЂйШчЭМ1жаЃЌЕБDFЃНADЪБЃЌЁїADFЪЧжсЖдГЦЭМаЮЃЎ
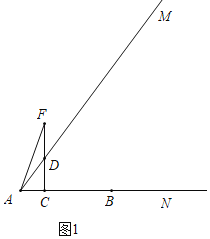
дђга5Љ3tЉ4tЃН5tЃЌНтЕУtЃН![]() ЃЌ
ЃЌ
ЂкШчЭМ2жаЃЌЕБAFЃНDFЪБЃЌЁїADFЪЧжсЖдГЦЭМаЮЃЎ
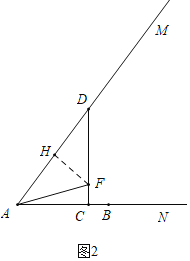
зїFHЁЭADЃЎ
ЁпFAЃНDFЃЌ
ЁрAHЃНDHЃН![]() tЃЌ
tЃЌ
гЩcos![]() ЃЌПЩЕУ
ЃЌПЩЕУ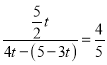 ЃЌНтЕУtЃН
ЃЌНтЕУtЃН![]() ЃЎ
ЃЎ
ЂлШчЭМ3жаЃЌЕБAFЃНDFЪБЃЌЁїADFЪЧжсЖдГЦЭМаЮЃЎ
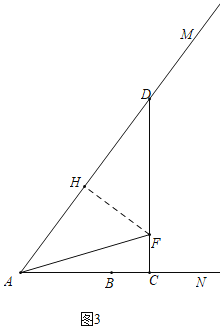
зїFHЁЭADЃЎ
ЁпFAЃНDFЃЌ
ЁрAHЃНDHЃН![]() tЃЌ
tЃЌ
гЩcosЁЯFDHЃН![]() ЃЌПЩЕУ
ЃЌПЩЕУ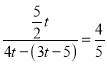 ЃЌНтЕУtЃН
ЃЌНтЕУtЃН![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФtЕФжЕЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ

 гХвэаЁАяЪжЭЌВНПкЫуЯЕСаД№АИ
гХвэаЁАяЪжЭЌВНПкЫуЯЕСаД№АИ