题目内容
如图,在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B.
求证:AB=AC+CD.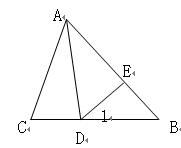
求证:AB=AC+CD.

见解析
试题分析:由∠1=∠B可根据等角对等边可得DE=BE,根据三角形外角的性质可得∠AED=2∠B,由∠C=2∠B可得∠AED=∠C,再结合AD平分∠CAB,公共边AD可得△CAD≌△EAD,从而可以证得结论。
∵∠1=∠B
∴DE=BE,∠AED=2∠B
∵∠C=2∠B
∴∠AED=∠C
∵AD平分∠CAB
∴∠CAD=∠BAD
又AD=AD
∴△CAD≌△EAD
∴AE=AC,CD=DE=EB
∴AB=AE+EB=AC+CD.
点评:解答本题的关键是掌握三角形外角的性质:三角形的一个外角等于不相邻的两个内角的和。同时熟练掌握全等三角形的对应边相等的性质。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


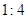 ,则这个等腰三角形顶角的度数为( )
,则这个等腰三角形顶角的度数为( )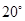
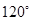




 ,则B=( )
,则B=( )




