题目内容
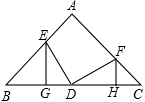
在Rt△ABC中,AC=3cm,AB=5cm,四边形CFDE为矩形,其中CF、CE在两直角边上.

(1)求BC的长度.
(2)设矩形的一边CF=xcm.当矩形ECFD是3㎝2,求矩形的长和宽是多少?

(1)求BC的长度.
(2)设矩形的一边CF=xcm.当矩形ECFD是3㎝2,求矩形的长和宽是多少?
(1)BC=4 ………………3分
(2)这个矩形的长是2cm,宽是1.5cm。
(2)这个矩形的长是2cm,宽是1.5cm。
试题分析:(1)由已知三角形ABC为直角三角形,AB为斜边,故根据斜边AB及直角边AC的长,利用勾股定理即可求出直角边AC的长;
(2).利用DE∥CF得出△ADE∽△ABC,从而得出
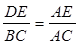 ,从而求出CE的表达式,然后根据矩形面积为3,列出一元二次方程式,然后求解即得。
,从而求出CE的表达式,然后根据矩形面积为3,列出一元二次方程式,然后求解即得。点评:此题要求熟练掌握勾股定理,相似三角形判定及性质定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 BD,E、F、G、H分别为AB、BC、CD、DA的中点.
BD,E、F、G、H分别为AB、BC、CD、DA的中点.
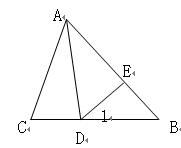
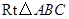 中,
中,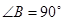 ,
,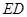 是
是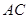 的垂直平分线,交
的垂直平分线,交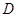 ,交
,交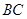 于点
于点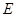 .已知
.已知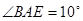 ,则
,则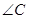 的度数为 ____________
的度数为 ____________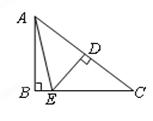
 ,两顶点
,两顶点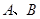 分别射线OM,ON上滑动,当∠OAB = 21°时, ∠NBC = 。滑动过程中,连结OC,则OC的长的最大值是 。
分别射线OM,ON上滑动,当∠OAB = 21°时, ∠NBC = 。滑动过程中,连结OC,则OC的长的最大值是 。
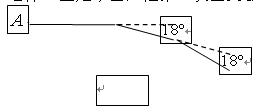
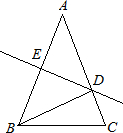
 中,
中,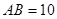 ,
,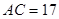 ,
, 边上的高为
边上的高为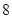 ,则
,则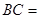
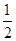 S△ABC;④EG+FH=
S△ABC;④EG+FH=