题目内容
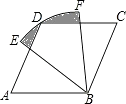
【题目】如图,已知△ABC是等边三角形,点D,E分别在边BC,AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 . (填写所有正确结论的序号)
【答案】①②③④
【解析】解:①正确.∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=60°,
∵DE=DC,
∴△DEC是等边三角形,
∴ED=EC=DC,∠DEC=∠AEF=60°,
∵EF=AE,
∴△AEF是等边三角形,
∴AF=AE,∠EAF=60°,
在△ABE和△ACF中,
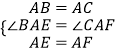 ,
,
∴△ABE≌△ACF,故①正确.
②正确.∵∠ABC=∠FDC,
∴AB∥DF,
∵∠EAF=∠ACB=60°,
∴AB∥AF,
∴四边形ABDF是平行四边形,
∴DF=AB=BC,故②正确.
③正确.∵△ABE≌△ACF,
∴BE=CF,S△ABE=S△AFC,
在△BCE和△FDC中,
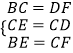 ,
,
∴△BCE≌△FDC,
∴S△BCE=S△FDC,
∴S△ABC=S△ABE+S△BCE=S△ACF+S△DCF,故③正确.
④正确.∵△BCE≌△FDC,
∴∠DBE=∠EFG,∵∠BED=∠FEG,
∴△BDE∽△FGE,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵BD=2DC,DC=DE,
∴ ![]() =2,
=2,
∴FG=2EG.故④正确.
【考点精析】本题主要考查了等边三角形的性质和平行四边形的判定与性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.

【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差 |
|
|
|
|
|
|
筐 数 |
|
|
|
|
|
|
(1)与标准质量比较,![]() 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价![]() 元,则出售这
元,则出售这![]() 筐白菜可卖多少元?
筐白菜可卖多少元?