题目内容
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/秒;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/秒,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为y(cm2),求y与t之间的函数关系式.
【答案】
(1)解:假设四边形PQCM是平行四边形,则PM∥QC,
∴AP:AB=AM:AC,
∵AB=AC,
∴AP=AM,即10﹣t=2t,
解得t= ![]() ,
,
∴当t= ![]() s时,四边形PQCM是平行四边形
s时,四边形PQCM是平行四边形
(2)解:∵PQ∥AC, 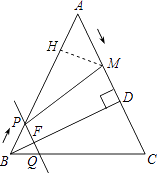
∴△PBQ∽△ABC,
∴△PBQ为等腰三角形,PQ=PB=t,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得BF= ![]() t,
t,
∴FD=BD﹣BF=8﹣ ![]() t,
t,
又∵MC=AC﹣AM=10﹣2t,
∴y= ![]() (PQ+MC)FD=
(PQ+MC)FD= ![]() (t+10﹣2t)(8﹣
(t+10﹣2t)(8﹣ ![]() t)=
t)= ![]() t2﹣8t+40.
t2﹣8t+40.
【解析】(1)四边形PQCM是平行四边形,得它的对边平行,进而得到AP=AM,列出关于t的方程,解方程即可求出答案;(2)根据PQ∥AC,可得△PBQ∽△ABC,根据相似三角形形状相似知道△PBQ为等腰三角形,即PQ=PB=t,再由相似三角形对应高的比等于相似比,用含t的式子就可以表示出FD,AM,CM,最后根据提醒的面积公式就能找出函数关系式。
【考点精析】本题主要考查了函数关系式和等腰三角形的性质的相关知识点,需要掌握用来表示函数关系的数学式子叫做函数解析式或函数关系式;等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目