ЬтФПФкШн
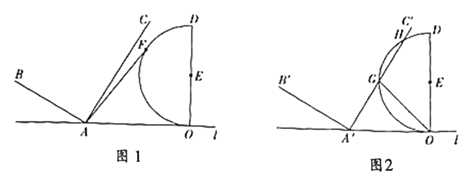
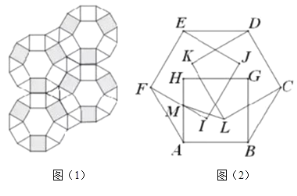
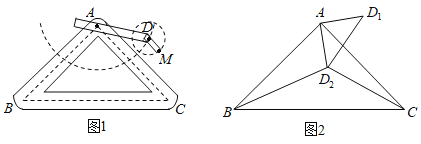
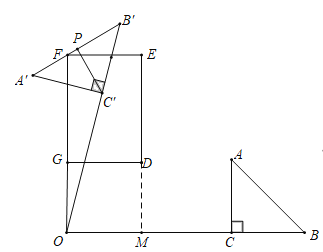
ЁОЬтФПЁПШчЭМ1ЃЌОиаЮDEFGжаЃЌDGЃН2ЃЌDEЃН3ЃЌRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌCAЃНCBЃН2ЃЌFGЃЌBCЕФбгГЄЯпЯрНЛгкЕуOЃЌЧвFGЁЭBCЃЌOGЃН2ЃЌOCЃН4ЃЎНЋЁїABCШЦЕуOФцЪБеыа§зЊІСЃЈ0ЁуЁмІСЃМ180ЁуЃЉЕУЕНЁїAЁфBЁфCЁфЃЎ
ЃЈ1ЃЉЕБІСЃН30ЁуЪБЃЌЧѓЕуCЁфЕНжБЯпOFЕФОрРыЃЎ
ЃЈ2ЃЉдкЭМ1жаЃЌШЁAЁфBЁфЕФжаЕуPЃЌСЌНсCЁфPЃЌШчЭМ2ЃЎ
ЂйЕБCЁфPгыОиаЮDEFGЕФвЛЬѕБпЦНааЪБЃЌЧѓЕуCЁфЕНжБЯпDEЕФОрРыЃЎ
ЂкЕБЯпЖЮAЁфPгыОиаЮDEFGЕФБпгаЧвжЛгавЛИіНЛЕуЪБЃЌЧѓИУНЛЕуЕНжБЯпDGЕФОрРыЕФШЁжЕЗЖЮЇЃЎ
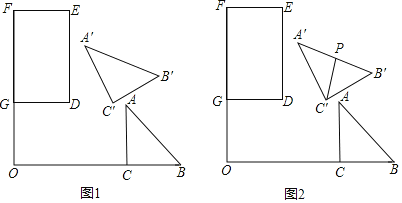
ЁОД№АИЁПЃЈ1ЃЉЕуCЁфЕНжБЯпOFЕФОрРыЮЊ2![]() ЃЛЃЈ2ЃЉЂйЕуCЁфЕНжБЯпDEЕФОрРыЮЊ2
ЃЛЃЈ2ЃЉЂйЕуCЁфЕНжБЯпDEЕФОрРыЮЊ2![]() +2ЃЛЂк2ЁмdЁм
+2ЃЛЂк2ЁмdЁм![]() Љ2ЛђdЃН3ЃЎ
Љ2ЛђdЃН3ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§ЕуCЁфзїCЁфHЁЭOFгкHЃЎИљОнжБНЧШ§НЧаЮЕФБпНЧЙиЯЕЃЌНтжБНЧШ§НЧаЮЧѓГіCHМДПЩЃЎ
ЃЈ2ЃЉЂйЗжСНжжЧщаЮЃКЕБCЁфPЁЮOFЪБЃЌЙ§ЕуCЁфзїCЁфMЁЭOFгкMЃЛЕБCЁфPЁЮDGЪБЃЌЙ§ЕуCЁфзїCЁфNЁЭFGгкNЃЎЭЈЙ§НтжБНЧШ§НЧаЮЃЌЗжБ№ЧѓГіCЁфMЃЌCЁфNМДПЩЃЎ
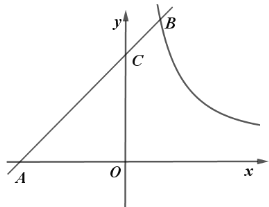
ЂкЩшdЮЊЫљЧѓЕФОрРыЃЎЕквЛжжЧщаЮЃКЕБЕуAЁфТфдкDEЩЯЪБЃЌСЌНгOAЁфЃЌбгГЄEDНЛOCгкMЃЎЕБЕуPТфдкDEЩЯЪБЃЌСЌНгOPЃЌЙ§ЕуPзїPQЁЭCЁфBЁфгкQЃЎНсКЯЭМЯѓПЩЕУНсТлЃЎ
ЕкЖўжжЧщаЮЃКЕБAЁфPгыFGЯрНЛЃЌВЛгыEFЯрНЛЪБЃЌЕБЕуAЁфдкFGЩЯЪБЃЌAЁфGЃН2![]() Љ2ЃЌМДdЃН2
Љ2ЃЌМДdЃН2![]() Љ2ЃЛЕБЕуPТфдкEFЩЯЪБЃЌЩшOFНЛAЁфBЁфгкQЃЌЙ§ЕуPзїPTЁЭBЁфCЁфгкTЃЌЙ§ЕуPзїPRЁЮOQНЛOBЁфгкRЃЌСЌНгOPЃЎЧѓГіQGПЩЕУНсТлЃЎ
Љ2ЃЛЕБЕуPТфдкEFЩЯЪБЃЌЩшOFНЛAЁфBЁфгкQЃЌЙ§ЕуPзїPTЁЭBЁфCЁфгкTЃЌЙ§ЕуPзїPRЁЮOQНЛOBЁфгкRЃЌСЌНгOPЃЎЧѓГіQGПЩЕУНсТлЃЎ
ЕкШ§жжЧщаЮЃКЕБAЁфPОЙ§ЕуFЪБЃЌДЫЪБЯдШЛdЃН3ЃЎзлЩЯЫљЪіМДПЩЕУНсТлЃЎ
НтЃКЃЈ1ЃЉШчЭМЃЌ
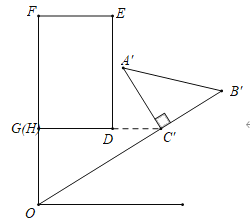
Й§ЕуCЁфзїCЁфHЁЭOFгкHЃЎ
ЁпЁїAЁфBЁфCЁфЪЧгЩЁїABCШЦЕуOФцЪБеыа§зЊЕУЕНЃЌ
ЁрCЁфO=CO=4ЃЌ
дкRtЁїHCЁфжаЃЌ
ЁпЁЯHCЁфOЃНІСЃН30ЁуЃЌ
ЁрCЁфHЃНCЁфOcos30ЁуЃН2![]() ЃЌ
ЃЌ
ЁрЕуCЁфЕНжБЯпOFЕФОрРыЮЊ2![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЂйШчЭМЃЌЕБCЁфPЁЮOFЪБЃЌЙ§ЕуCЁфзїCЁфMЁЭOFгкMЃЎ
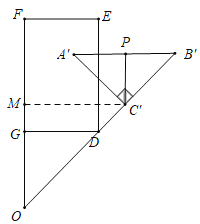
ЁпЁїAЁфBЁфCЁфЮЊЕШбќжБНЧШ§НЧаЮЃЌPЮЊAЁфBЁфЕФжаЕуЃЌ
ЁрЁЯAЁфCЁфP=45ЁуЃЌ
ЁпЁЯAЁфBЁфO=90ЁуЃЌ
ЁрЁЯOCЁфP=135Ёу.
ЁпCЁфPЁЮOFЃЌ
ЁрЁЯOЃН180ЁуЉЁЯOCЁфPЃН45ЁуЃЌ
ЁрЁїOCЁфMЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁпOCЁфЃН4ЃЌ
ЁрCЁфMЃНCЁфOcos45Ёу=4ЁС![]() =
=![]() ЃЌ
ЃЌ
ЁрЕуCЁфЕНжБЯпDEЕФОрРыЮЊ![]() ЃЎ
ЃЎ
ШчЭМЃЌЕБCЁфPЁЮDGЪБЃЌЙ§ЕуCЁфзїCЁфNЁЭFGгкNЃЎ
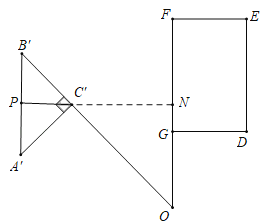
ЭЌЗЈПЩжЄЁїOCЁфNЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрCЁфNЃН![]() ЃЌ
ЃЌ
ЁпGD=2ЃЌ
ЁрЕуCЁфЕНжБЯпDEЕФОрРыЮЊ![]() ЃЎ
ЃЎ
ЂкЩшdЮЊЫљЧѓЕФОрРыЃЎ
ЕквЛжжЧщаЮЃКШчЭМЃЌЕБЕуAЁфТфдкDEЩЯЪБЃЌСЌНгOAЁфЃЌбгГЄEDНЛOCгкMЃЎ
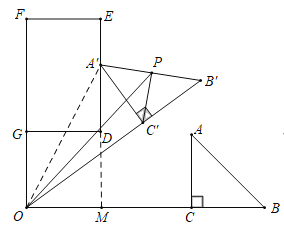
ЁпOC=4ЃЌAC=2ЃЌЁЯACO=90ЁуЃЌ
![]()
ЁпOMЃН2ЃЌЁЯOMAЁфЃН90ЁуЃЌ
ЁрAЁфMЃН![]() ЃН
ЃН![]() ЃН4ЃЌ
ЃН4ЃЌ
гжЁпOG=2ЃЌ
ЁрDM=2ЃЌ
ЁрAЁфDЃНAЁфM-DM=4-2=2ЃЌ
МДdЃН2ЃЌ
ШчЭМЃЌЕБЕуPТфдкDEЩЯЪБЃЌСЌНгOPЃЌЙ§ЕуPзїPQЁЭCЁфBЁфгкQЃЎ
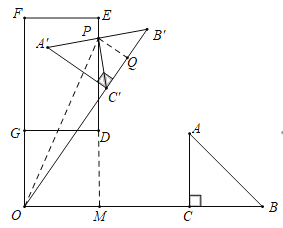
ЁпPЮЊAЁфBЁфЕФжаЕуЃЌЁЯAЁфCЁфBЁф=90ЁуЃЌ
ЁрPQЁЮAЁфCЁфЃЌ
Ёр![]()
ЁпBЁфCЁф=2
ЁрPQЃН1ЃЌCQ=1ЃЌ
ЁрQЕуЮЊBЁфCЁфЕФжаЕуЃЌвВЪЧа§зЊЧАBCЕФжаЕуЃЌ
ЁрOQ=OC+CQ=5
ЁрOPЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрPMЃН![]() ЃЌ
ЃЌ
ЁрPDЃН![]() ЃЌ
ЃЌ
ЁрdЃН![]() Љ2ЃЌ
Љ2ЃЌ
Ёр2ЁмdЁм![]() Љ2ЃЎ
Љ2ЃЎ
ЕкЖўжжЧщаЮЃКЕБAЁфPгыFGЯрНЛЃЌВЛгыEFЯрНЛЪБЃЌЕБЕуAЁфдкFGЩЯЪБЃЌAЁфGЃН2![]() Љ2ЃЌМДdЃН2
Љ2ЃЌМДdЃН2![]() Љ2ЃЌ
Љ2ЃЌ
ШчЭМЃЌЕБЕуPТфдкEFЩЯЪБЃЌЩшOFНЛAЁфBЁфгкQЃЌЙ§ЕуPзїPTЁЭBЁфCЁфгкTЃЌЙ§ЕуPзїPRЁЮOQНЛOBЁфгкRЃЌСЌНгOPЃЎ
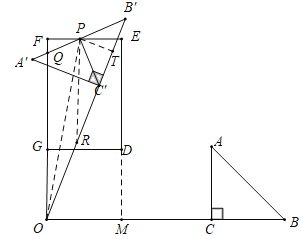
гЩЩЯПЩжЊOPЃН![]() ЃЌOFЃН5ЃЌ
ЃЌOFЃН5ЃЌ
ЁрFPЃН![]() ЃН
ЃН![]() ЃН1ЃЌ
ЃН1ЃЌ
ЁпOFЃНOTЃЌPFЃНPTЃЌЁЯFЃНЁЯPTOЃН90ЁуЃЌ
ЁрRtЁїOPFЁеRtЁїOPTЃЈHLЃЉЃЌ
ЁрЁЯFOPЃНЁЯTOPЃЌ
ЁпPQЁЮOQЃЌ
ЁрЁЯOPRЃНЁЯPOFЃЌ
ЁрЁЯOPRЃНЁЯPORЃЌ
ЁрORЃНPRЃЌ
ЁпPT2+TR2ЃНPR2ЃЌ
![]()
ЁрPRЃН2.6ЃЌRTЃН2.4ЃЌ
ЁпЁїBЁфPRЁзЁїBЁфQOЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрOQЃН![]() ЃЌ
ЃЌ
ЁрQGЃНOQЉOGЃН![]() ЃЌМДdЃН
ЃЌМДdЃН![]()
Ёр2![]() Љ2ЁмdЃМ
Љ2ЁмdЃМ![]() ЃЌ
ЃЌ
ЕкШ§жжЧщаЮЃКЕБAЁфPОЙ§ЕуFЪБЃЌШчЭМЃЌ
ДЫЪБFG=3ЃЌМДdЃН3ЃЎ
злЩЯЫљЪіЃЌ2ЁмdЁм![]() Љ2ЛђdЃН3ЃЎ
Љ2ЛђdЃН3ЃЎ

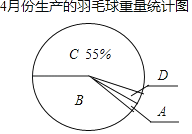
ЁОЬтФПЁПвЛжЛг№УЋЧђЕФжиСПКЯИёБъзМЪЧ5.0ПЫЁЋ5.2ПЫЃЈКЌ5.0ПЫЃЌВЛКЌ5.2ПЫЃЉЃЌФГГЇЖд4дТЗнЩњВњЕФг№УЋЧђжиСПНјааГщбљМьбщЃЎВЂНЋЫљЕУЪ§ОнЛцжЦГЩШчЭМЭГМЦЭМБэЃЎ
4дТЗнЩњВњЕФг№УЋЧђжиСПЭГМЦБэ
зщБ№ | жиСПxЃЈПЫЃЉ | Ъ§СПЃЈжЛЃЉ |
A | xЃМ5.0 | m |
B | 5.0ЁмxЃМ5.1 | 400 |
C | 5.1ЁмxЃМ5.2 | 550 |
D | xЁн5.2 | 30 |
ЃЈ1ЃЉЧѓБэжаmЕФжЕМАЭМжаBзщЩШаЮЕФдВаФНЧЕФЖШЪ§ЃЎ
ЃЈ2ЃЉЮЪетаЉГщбљМьбщЕФг№УЋЧђжаЃЌКЯИёТЪЪЧЖрЩйЃПШчЙћЙКЕУ4дТЗнЩњВњЕФг№УЋЧђ10ЭВЃЈУПЭВ12жЛЃЉЃЌЙРМЦЫљЙКЕУЕФг№УЋЧђжаЃЌЗЧКЯИёЦЗЕФг№УЋЧђгаЖрЩйжЛЃП