Question

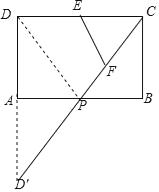
【题目】如图，矩形△ABCD中，AB＝2，AD＝1，E为CD中点，P为AB边上一动点（含端点），F为CP中点，则△CEF的周长最小值为_____．

Answer 1

【答案】 +1．

【解析】

根据三角形的中位线的性质得到EF＝PD，得到C△CEF＝CE+CF+EF＝CE+（CP+PD）＝（CD+PC+PD）＝C△CDP，当△CDP的周长最小时，△CEF的周长最小；即PC+PD的值最小时，△CEF的周长最小；如图，作D关于AB的对称点D′，连接CD′交AB于P，于是得到结论．

解：∵E为CD中点，F为CP中点，

∴EF＝PD，

∴C△CEF＝CE+CF+EF＝CE+（CP+PD）＝（CD+PC+PD）＝C△CDP，

∴当△CDP的周长最小时，△CEF的周长最小；

即PC+PD的值最小时，△CEF的周长最小；

如图，作D关于AB的对称点D′，连接CD′交AB于P，

∵AD＝AD′＝BC，AD′∥BC，

∴四边形AD′BC是平行四边形，

∴AP＝PB＝1，PD′＝PC，

∴CP＝PD＝，

∴C△CEF＝C△CDP＝+1，

故答案为： +1．