题目内容
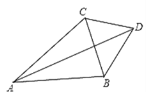
【题目】如图,在△ABC中,∠BAC=40°,∠ACB=60°,D为△ABC外一点,DA平分∠BAC,且CBD=50°,则∠DCB的度数是_______.
【答案】60°
【解析】
如图,延长AB到P,延长AC到Q,作DH⊥AP于H,DE⊥AQ于E,DF⊥BC于F.想办法证明DE=DF,推出DC平分∠QCB即可解决问题.
解:如图,延长AB到P,延长AC到Q,作DH⊥AP于H,DE⊥AQ于E,DF⊥BC于F.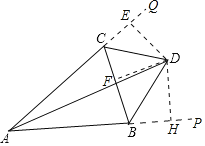
∵∠PBC=∠BAC+∠ACB=40°+60°=100°,∠CBD=50°,
∴∠DBC=∠DBH,
∵DF⊥BC,DH⊥BP,
∴DF=DH,
又∵DA平分∠PAQ,DH⊥PA,DE⊥AQ,
∴DE=DH,
∴DE=DF,
∴CD平分∠QCB,
∵∠QCB=180°-60°=120°,
∴∠DCB=60°,
故答案为60°.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目





