题目内容
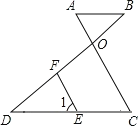
【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.

【答案】15°
【解析】∵BD、CD分别平分∠ABC、∠ACB,∠A=60°,
∴∠DBC=![]() ∠ABC,∠DCB=
∠ABC,∠DCB=![]() ∠ACB,
∠ACB,
∴∠DBC+∠DCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-∠A)=
(180°-∠A)=![]() ×(180°-60°)=60°,
×(180°-60°)=60°,
∴∠MBC+∠NCB=360°-60°=300°,
∵BE、CE分别平分∠MBC、∠BCN,
∴∠5+∠6=![]() ∠MBC,∠1=
∠MBC,∠1=![]() ∠NCB,
∠NCB,
∴∠5+∠6+∠1=![]() (∠NCB+∠NCB)=150°,
(∠NCB+∠NCB)=150°,
∴∠E=180°-(∠5+∠6+∠1)=180°-150°=30°,
∵BF、CF分别平分∠EBC、∠ECQ,
∴∠5=∠6,∠2=∠3+∠4,
∵∠3+∠4=∠5+∠F,∠2+∠3+∠4=∠5+∠6+∠E,
即∠2=∠5+∠F,2∠2=2∠5+∠E,
∴2∠F=∠E,
∴∠F=![]() ∠E=
∠E=![]() ×30°=15°.
×30°=15°.
故答案是:15°.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目