��Ŀ����
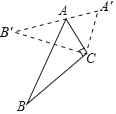
����Ŀ����A��B�������ϱ�ʾ������ͼ��ʾ������P�ӵ�A������������������ÿ��1����λ���ȵ��ٶ����B�˶�����Bֹͣ�˶���ͬʱ������Q�ӵ�B������������������ÿ��2����λ���ȵ��ٶ����A�˶�������Aֹͣ�˶����P�˶���ʱ��Ϊt�룬P��Q����ľ���Ϊd��d��0������λ���ȣ�
��1����t��1ʱ��d���� ����
��2����P��Q��������һ����ǡ���˶����߶�AB���е�ʱ����d��ֵ��
��3������P�˶����߶�AB��3�ȷֵ�ʱ��ֱ��д��d��ֵ��
��4����d��5ʱ��ֱ��д��t��ֵ��
![]()
���𰸡���1��d��3����2��d��ֵΪ3��![]() ����3������d��ֵΪ0��4����4������t��ֵΪ
����3������d��ֵΪ0��4����4������t��ֵΪ![]() ��5��
��5��
��������
��1����t��1ʱ�����AP��1��BQ��2������PQ��AB��AP��BQ������⣻
��2������P��ǡ���˶����߶�AB���е㣻��Q��ǡ���˶����߶�AB���е���������������ۣ�
��3������P�˶����߶�AB��3�ȷֵ�ʱ������AP��![]() AB����AP��
AB����AP��![]() AB��������������ۣ�
AB��������������ۣ�
��4����d��5ʱ������P��Q����֮ǰ����P��Q����֮����������������ۣ�
��1����t��1ʱ��AP��1��BQ��2��
��AB��4������2����6��
��PQ��AB��AP��BQ��3����d��3��
�ʴ�Ϊ3��
��2���߶�AB���е��ʾ�����ǣ�![]() ��1��
��1��
�����P��ǡ���˶����߶�AB���е㣬��ôAP��![]() AB��3��t��
AB��3��t��![]() ��3��
��3��
BQ��2��3��6����Q�˶���A�㣬
��ʱd��PQ��PA��3��
�����Q��ǡ���˶����߶�AB���е㣬��ôBQ��![]() AB��3��t��
AB��3��t��![]() ��
��
AP��1��![]() ��
��![]() ��
��
��d��PQ��AB��AP��BQ��6��![]() ��3��
��3��![]() ��
��
��d��ֵΪ3��![]() ��
��
��3������P�˶����߶�AB��3�ȷֵ�ʱ�������������
�����AP��![]() AB��2����ôt��
AB��2����ôt��![]() ��2��
��2��
��ʱBQ��2��2��4��P��Q�غ���ԭ�㣬
��d��PQ��0��
�����AP��![]() AB��4����ôt��
AB��4����ôt��![]() ��4��
��4��
�߶���Q�ӵ�B������������������ÿ��2����λ���ȵ��ٶ����A�˶�������Aֹͣ�˶���
���ʱBQ��6����Q�˶���A�㣬
��d��PQ��AP��4��
������d��ֵΪ0��4��
��4����d��5ʱ�������������
��P��Q����֮ǰ��
��PQ��AB��AP��BQ��
��6��t��2t��5��
���t��![]() ��
��
��P��Q����֮��
��P���˶����߶�AB���е�ʱ��t��3����ʱQ�˶���A�㣬ֹͣ�˶���
��d��AP��t��5��
������t��ֵΪ![]() ��5��
��5��