题目内容
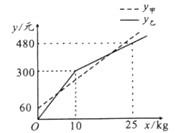
【题目】师徒二人各加工同样多的零件,师父每小时加工200个,徒弟每小时加工125个.若徒弟先加工段时间之后,师父才开始工作师父工作2小时后发现自己加工的零件个数和徒弟加工的个数刚好相同,如图是师徒两人完成的零件个数之差y(个)与徒弟工作的时间x(小时)之间的函数图象,根据图象回答问题:
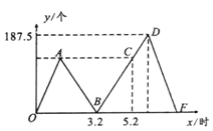
(1)求出点A的坐标,并解释该点坐标表示的实际意义;
(2)求出线段BD的函数表达式;
(3)求徒弟这次加工的零件总数
【答案】(1)A (1.2,150),徒弟工作了1.2小时后师父开始工作,此时徒弟比师父提前完成了150个;(2)y=75x-240(3.2≤x≤5.7);(3)徒弟这次加工的零件总数是900个
【解析】
(1)图象从A点开始出现转折,师徒两人完成的零件数之差减小,说明师父开始工作,再利用师父工作2小时后加工的零件数与徒弟相同即可求出A点的横坐标,再根据徒弟加工的零件数即可求出A点的纵坐标;
(2)已知B,C的坐标,用待定系数法即可求出直线BC的解析式,从而根据D点的纵坐标确定D的横坐标,进而确定线段BD的函数表达式及自变量的范围;
(3)根据D点坐标可求出师父工作的时间和加工的零件数量,因为最后使徒两人加工的零件数之差为零,所以徒弟加工的零件数量等于师父的零件数,从而可得出答案.
(1)解:由图象知,当x=3.2时,y=0.即徒弟工作3.2小时后,师徒两人加工零件个数刚好相同.
此时师父工作了2小时,故徒弟提前工作的时间是:3.2-2=1.2(时),
徒弟提前完成的零件个数:1.2×125=150(个)
点A的坐标是(1.2,150)
实际意义:徒弟工作了1.2小时后师父开始工作,此时徒弟比师父提前完成了150个
(2)解:由图象易得点C坐标为(5.2,150),
设直线BC的函数表示式为y=kx+b,其过(5.2,150),(3.2,0),
易得 ![]() ,解得
,解得 ![]()
故:y=75x-240,
当y=187.5时,代入得:75x-240=187.5,解得x=5.7,
故线段BD的函数表达式:y=75x-240(3.2≤x≤5.7)
(3)解:由(2)得点D的坐标(5.7,187.5).
根据图象得师父完成工作共需的时间是:
5.7-1.2=4.5(小时),加工零件的个数是4.5×200=900(个),
又师徒二人加工的零件个数相同,所以徒弟加工了900个
答:徒弟这次加工的零件总数是900个.