题目内容
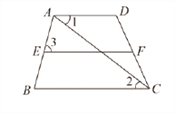
【题目】如图,□ABCD中,E是BC边的中点,连接AE,F为CD边上一点,且满足∠DFA=2∠BAE.

(1)若∠D=105°,∠DAF=35°.求∠FAE的度数;
(2)求证:AF=CD+CF.
【答案】(1)20°;(2)见解析
【解析】试题分析:(1)根据平行四边形的性质、平行线的性质证得![]() ;然后结合已知条件
;然后结合已知条件![]() 求得
求得![]() 从而求得
从而求得![]() 的度数;
的度数;
(2)在AF上截取![]() 连接
连接![]() 利用全等三角形的判定定理SAS证得
利用全等三角形的判定定理SAS证得![]() ≌
≌![]() ,由全等三角形的对应角相等、对应边相等
,由全等三角形的对应角相等、对应边相等![]() ;然后由中点E的性质平行线的性质以及等腰三角形的判定与性质求得
;然后由中点E的性质平行线的性质以及等腰三角形的判定与性质求得![]() 最后根据线段间的和差关系证得结论.
最后根据线段间的和差关系证得结论.
试题解析: ![]()
![]() (三角形内角和定理).
(三角形内角和定理).
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD(平行四边形对边平行且相等).
![]() (两直线平行,内错角相等);
(两直线平行,内错角相等);
![]() (已知),
(已知),
![]() (等量代换).
(等量代换).
即![]()
![]()
![]()
![]()
(2) 证明:在AF上截取![]() 连接
连接![]()
![]()
∴![]() ≌
≌![]() ,
,
又∵E为BC中点,
![]()
![]()
∵AB∥CD, ![]()
又![]()
![]()
又![]()
![]()
又![]()
![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目