题目内容
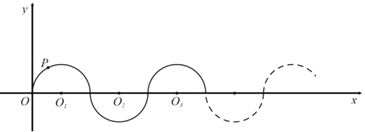
【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆![]() ,
,![]() ,
,![]() ,…组成一条平滑的曲线.点
,…组成一条平滑的曲线.点![]() 从原点
从原点![]() 出发,沿这条曲线向右运动,速度为每秒
出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2002秒时点
个单位长度,则第2002秒时点![]() 的坐标为____.
的坐标为____.
【答案】![]()
【解析】
由半圆的半径以及部分点P的坐标可找出规律P8n(8n×![]() ,0)P8n+1((8n+1)×
,0)P8n+1((8n+1)×![]() ,
,![]() ),P8n+2((8n+2)×
),P8n+2((8n+2)×![]() ,1),P8n+3((8n+3)
,1),P8n+3((8n+3)![]() ,
,![]() ),P8n+4((8n+4)
),P8n+4((8n+4)![]() ,0),P8n+5((8n+5)×
,0),P8n+5((8n+5)×![]() ,-
,-![]() ),P8n+6((8n+6)×
),P8n+6((8n+6)×![]() ,-1),P8n+7((8n+7)×
,-1),P8n+7((8n+7)×![]() ,-
,-![]() ),P8n+8((8n+8)×
),P8n+8((8n+8)×![]() ,1),根据本规律即可得解答..
,1),根据本规律即可得解答..
解:以时间为点P的下标.
观察可以发现规律:P0(0,0),P1(![]() ,
,![]() ),P2(1,1),P3(1
),P2(1,1),P3(1![]() ,
,![]() ),P4(2,0),P5(5×
),P4(2,0),P5(5×![]() ,-
,-![]() ),P6(6×
),P6(6×![]() ,-1),P7(7×
,-1),P7(7×![]() ,-
,-![]() ),…P8n(8n×
),…P8n(8n×![]() ,0)P8n+1((8n+1)×
,0)P8n+1((8n+1)×![]() ,
,![]() ),P8n+2((8n+2)×
),P8n+2((8n+2)×![]() ,1),P8n+3((8n+3)
,1),P8n+3((8n+3)![]() ,
,![]() ),P8n+4((8n+4)
),P8n+4((8n+4)![]() ,0),P8n+5((8n+5)×
,0),P8n+5((8n+5)×![]() ,-
,-![]() ),P8n+6((8n+6)×
),P8n+6((8n+6)×![]() ,-1),P8n+7((8n+7)×
,-1),P8n+7((8n+7)×![]() ,-
,-![]() ),P8n+8((8n+8)×
),P8n+8((8n+8)×![]() ,1).
,1).
∵2002=8×250+2,
∴.第2002秒时,点P的坐标是(2002×![]() , 1)即(1001,1).
, 1)即(1001,1).
故答案为(1001,1).

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目