��Ŀ����
����Ŀ����֪![]() ����
����![]() �ĺ������±���
�ĺ������±���![]() ��
��![]() �ļ����Ӧֵ��
�ļ����Ӧֵ��

С�ϸ���ѧϰ�����ľ��飬����������������ӳ����![]() ��
��![]() ֮��ı仯���ɣ��ֱ�Ժ���
֮��ı仯���ɣ��ֱ�Ժ���![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
������С�ϵ�̽�����̣��벹��������
��1����ͼ����ͬһƽ��ֱ������ϵ![]() �У�����ϱ��и�����ֵ����Ӧ�ĵ�
�У�����ϱ��и�����ֵ����Ӧ�ĵ�![]() ������������
������������![]() ��ͼ��
��ͼ��

��2����ϻ����ĺ���ͼ������⣺
�ٵ�![]() ʱ����Ӧ�ĺ���ֵ
ʱ����Ӧ�ĺ���ֵ![]() ԼΪ_________��
ԼΪ_________��
��д������![]() ��һ�����ʣ�_________________________��
��һ�����ʣ�_________________________��
�۵�![]() ʱ��
ʱ��![]() ��ȡֵ��Χ��_________________________��
��ȡֵ��Χ��_________________________��
���𰸡���1�������ͼ����������2����3.13���ڵ�![]() ʱ��
ʱ��![]() ����Сֵ
����Сֵ![]() ����
����![]() ����
����![]() ��
��
��������
(1)���ݸ����Ķ�Ӧ��ֵ�����ͼ���ɣ�(2)�ٸ���ͼ�ι۲�ɵô𰸣��ڸ���ͼ��ó����ʼ��ɣ��۹۲�ͼ�����ú���ֵ�Ĵ�Сȷ���Ա�����ȡֵ��Χ���ɣ�
�⣺�����ͼ���£�
��1����ͼ��
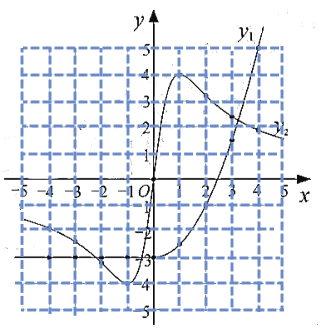
��2���۲�ͼ��ã���3.13��
�ڵ�![]() ʱ��
ʱ��![]() ����Сֵ
����Сֵ![]() ��
��
��![]() ����
����![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ʱ��
ʱ��![]() ����Сֵ
����Сֵ![]() ��
��![]() ����
����![]() ��
��

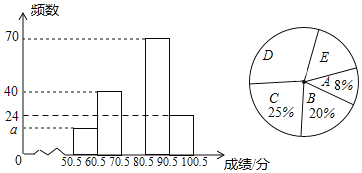
 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�����Ŀ������ѧ��Ͷ����ÿ��Ͷ10�Σ�ͳ������ÿ��Ͷ�еĴ������õ�������ݣ��������ݽ��������ͷ�������������Ϣ��
ƽ���� | ��λ�� | ���� |
m | 6 | 7 |
������ѡ����ȷ���ǣ� ��
A.���ܻ���ѧ��Ͷ����8��
B.�������֮�͵����ֵ����Ϊ30
C.�������֮�͵���Сֵ����Ϊ20
D.ƽ����mһ������![]()