Question

【题目】如图，一次函数y=-x+4的图象与反比例函数y=（k为常数，且k≠0）的图象交于A（1，a），B两点．

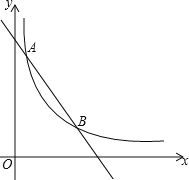
（1）求反比例函数的表达式及点B的坐标；

（2）结合图象直接写出不等式-x+4＞的解集

（3）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标及△PAB的面积．

Answer 1

【答案】（1）反比例函数的表达式（x≠0），B点坐标为（3，1）；（2）1<x<3；（3）满足条件的P点坐标为（2.5，0），此时△PAB的面积面积为1.5．

【解析】

（1）依据点A为直线和曲线的交点，代入函数解析式即可得出结论，同时联立方程组即可求得B点的坐标；

（2）图象在上面的y值大，联系函数解析式即可直接得出不等式的解集；

（3）找B点关于x轴的对称点C，连接AC与x轴交于P点，此点即使所求之点，根据S△PAB = S△PAD － S△PDB，即可得到结论．

（1）∵点A（1，a）是一次函数y=﹣x+4与反比例函数y（k为常数，且k≠0）的交点，∴，解得：a=k=3，∴反比例函数的表达式y，解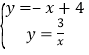得：A（1，3），B（3，1），故反比例函数的表达式y（x≠0），B点坐标为（3，1）．

（2）由图象知，当1＜x＜3时，直线图象在曲线的上方，故不等式﹣x+4的解集为1＜x＜3．

（3）找B点关于x轴的对称点C，连接AC交x轴于P点，如图：

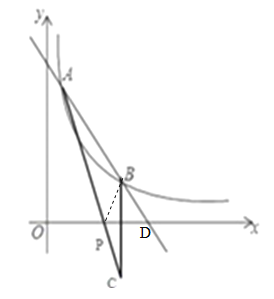
由（2）可知C点坐标为（3，﹣1）．

∵PC=PB，A、P、C在一条直线上，所以此时PA+PB最短，设直线AC方程为y=bx+c，则有，解得：b=﹣2，c=5，故直线AC方程为y=﹣2x+5，将y=0代入其中得：x=2.5，故得出P点坐标为（2.5，0）．

在y=﹣x+4中，令y=0，解得：x=4，∴D（4，0），∴PD=OD-OP=4-2.5=1.5.S△PAB = S△PAD － S△PDB=PD|yA|－PD|yB|=×1.5×（3-1）=1.5．

答：满足条件的P点坐标为（2.5，0），此时△PAB的面积面积为1.5．