Question

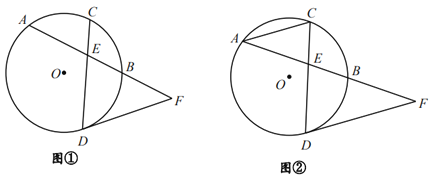
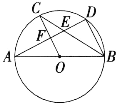
【题目】如图所示，AB是⊙O的直径，C、D是⊙O上的点，且OC∥BD, AD分别与BC，OC相交于点E，F，则下列结论：①AD⊥BD; ②∠AOC=∠AEC; ③CB平分∠ABD;④AF=DF; ⑤BD=2OF; ⑥△CEF ≌△BED,其中一定成立的是（ ）

A. ① ③ ⑤ ⑥ B. ① ③ ④ ⑤

C. ② ④ ⑤ ⑥ D. ② ③ ④ ⑥

Answer 1

【答案】B

【解析】

①由直径所对圆周角是直角可以判断，②由于∠AOC是⊙O的圆心角，∠AEC是⊙O的圆内部的角，由此可以判断，③由平行线得到∠OCB=∠DBC，再由同圆的半径相等得到结论判断出∠OBC=∠DBC；

④用半径垂直于不是直径的弦，必平分弦判断；

⑤用三角形的中位线可以得到结论；

⑥得不到△CEF和△BED中对应相等的边，所以不一定全等．

①∵AB是⊙O的直径，∴∠ADB=90°，∴AD⊥BD，故①正确；

②∵∠AOC是⊙O的圆心角，∠AEC是⊙O的圆内部的角，∴∠AOC≠∠AEC，故②不正确；

③∵OC∥BD，∴∠OCB=∠DBC．

∵OC=OB，∴∠OCB=∠OBC，∴∠OBC=∠DBC，∴BC平分∠ABD，故③正确；

④∵AB是⊙O的直径，∴∠ADB=90°，∴AD⊥BD．

∵OC∥BD，∴∠AFO=90°．

∵点O为圆心，∴AF=DF，故④正确；

⑤由④有，AF=DF．

∵点O为AB中点，∴OF是△ABD的中位线，∴BD=2OF，故⑤正确；

⑥∵△CEF和△BED中，没有相等的边，∴△CEF与△BED不全等，故⑥不正确；

综上可知：其中一定成立的有①③④⑤．

故选B．