Question

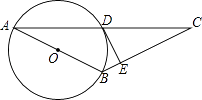
【题目】如图，点O为坐标原点，点A的坐标为（3，0），点B的坐标为（0，4），⊙D过A，B，O三点，点C为 上的一点（不与O、A两点重合），连接OC，AC，则cosC的值为（ ）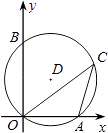
A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：连接AB， ∵点A的坐标为（3，0），点B的坐标为（0，4），
∴AO=3，BO=4，
∴AB=5，
∵∠C=∠OBA，
∴cosC的值为：cos∠OBA= = ．
故选：D．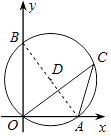

【考点精析】利用圆周角定理和解直角三角形对题目进行判断即可得到答案，需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．