��Ŀ����
����Ŀ���졢�������ֱ�����180ǧ�ļס�������ͬʱ��������ͬһ·��������ʻ��������У��쳵�����ҵ�ͣ��һ��ʱ���ԭ·ԭ�ٷ��ؼأ���������رȿ쳵������� ![]() Сʱ�������ٶ��ǿ쳵�ٶȵ�һ�룬�졢����������غ�ֹͣ��ʻ����������Գ����ص�·��y��ǧ�ף�������ʱ��x��Сʱ���ĺ���ͼ����ͼ��ʾ������ͼ����Ϣ����������⣺
Сʱ�������ٶ��ǿ쳵�ٶȵ�һ�룬�졢����������غ�ֹͣ��ʻ����������Գ����ص�·��y��ǧ�ף�������ʱ��x��Сʱ���ĺ���ͼ����ͼ��ʾ������ͼ����Ϣ����������⣺ 
��1����ֱ��д���졢���������ٶȣ�
��2����쳵���ع�����y��ǧ�ף���x��Сʱ���ĺ�����ϵʽ��
��3�������������ʱ�����90ǧ��·�̣�ֱ��д���𰸣�
���𰸡�
��1���⣺�쳵�ٶȣ�180��2�£� ![]() -
- ![]() ��=120ǧ��/ʱ��
��=120ǧ��/ʱ��
�����ٶȣ�120��2=60ǧ��/ʱ
��2���⣺�쳵ͣ����ʱ�䣺 ![]() ��
�� ![]() ��2=
��2= ![]() ��Сʱ����
��Сʱ����
![]() +
+ ![]() =2��Сʱ������C��2��180����
=2��Сʱ������C��2��180����
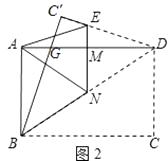
��CD�Ľ���ʽΪ��y=kx+b����
��C��2��180����D�� ![]() ��0�����룬��
��0�����룬��
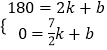 ��
��
��� ![]() ��
��
��쳵���ع�����y��ǧ�ף���x��Сʱ���ĺ�����ϵʽΪy=��120x+420��2��x�� ![]() ��
��
��3���⣺����֮ǰ��120x+60x+90=180��
���x= ![]() ��
��
����֮��120x+60x��90=180��
���x= ![]() ��
��
�쳵�Ӽص��ҵ���Ҫ180��120= ![]() Сʱ��
Сʱ��
�쳵����֮��60x=90+120��x�� ![]() ��
�� ![]() ��
��
���x= ![]()
�������������������� ![]() ��
�� ![]() ��
�� ![]() Сʱ���90ǧ��·�̣�
Сʱ���90ǧ��·�̣�
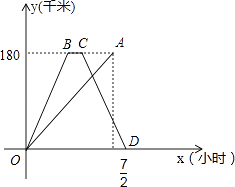
����������1������·������Ӧ��ʱ�䣬��ÿ쳵���������ٶȣ���2������õ�C�����꣬�ٸ��ݵ�D�����꣬���ô���ϵ�������CD�Ľ���ʽ����3�����������������������֮ǰ������������֮���ڿ쳵����֮�ֱ����ʱ�伴�ɣ�