��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx��2��x�ύ�ڵ�A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C��0����2����OB=4OA��tan��BCO=2��
��1����A��B��������ꣻ
��2���������ߵĽ���ʽ��
��3����M��N�ֱ����߶�BC��AB�ϵĶ��㣬��M�ӵ�B������ÿ��![]() ����λ���ٶ����C�˶���ͬʱ��N�ӵ�A������ÿ��2����λ���ٶ����B�˶�������M��N�е�һ�㵽���յ�ʱ������ͬʱֹͣ�˶�������M��MP��x���ڵ�E�����������ڵ�P�����M����N���˶�ʱ��Ϊt��s������tΪ����ʱ����PNE�ǵ��������Σ�
����λ���ٶ����C�˶���ͬʱ��N�ӵ�A������ÿ��2����λ���ٶ����B�˶�������M��N�е�һ�㵽���յ�ʱ������ͬʱֹͣ�˶�������M��MP��x���ڵ�E�����������ڵ�P�����M����N���˶�ʱ��Ϊt��s������tΪ����ʱ����PNE�ǵ��������Σ�

���𰸡���1��A����1��0������2��y=![]() x2��
x2��![]() x��2����3����t=1ʱ����PNE�ǵ��������Σ�
x��2����3����t=1ʱ����PNE�ǵ��������Σ�
��������
��1����C��0����2��֪OC=2������tan��BCO=![]() =2��OB=4���ݴ˵ó���B���꣬����OB=4OA�ɵõ�A���ꣻ
=2��OB=4���ݴ˵ó���B���꣬����OB=4OA�ɵõ�A���ꣻ
��2������A��B������������߽���ʽ���a��b��ֵ���Ӷ��ó��𰸣�
��3��������֪AN=2t��BM=![]() t������tan��BME=tan��BCO=2֪
t������tan��BME=tan��BCO=2֪![]() =
=![]() �����OE=OB��BE=4��t���Ӷ��ó�PE=��
�����OE=OB��BE=4��t���Ӷ��ó�PE=��![]() ��4��t��2+
��4��t��2+![]() ��4��t��+2���ٷֵ�N�ڵ�E�����Ҳ������������ʾ��NE�ij�������NE=PE�з������ɵô𰸣�
��4��t��+2���ٷֵ�N�ڵ�E�����Ҳ������������ʾ��NE�ij�������NE=PE�з������ɵô𰸣�
��1����C��0����2����
��OC=2��
��tan��BCO=![]() =2��OB=4��
=2��OB=4��
���B��4��0����
��OB=4OA��
��OA=1��
��A����1��0����
��2������A����1��0����B��4��0������y=ax2+bx��2��
�ã�![]() ��
��
��ã�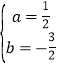 ��
��
�������߽���ʽΪy=![]() x2��
x2��![]() x��2��
x��2��
��3�����M����N���˶�ʱ��Ϊt��s������AN=2t��BM=![]() t��
t��
��PE��x�ᣬ
��PE��OC��
���BME=��BCO��
��tan��BME=tan��BCO����![]() =2��
=2��
��![]() =
=![]() ����
����![]() =
=![]() ��
��
��BE=t��
��OE=OB��BE=4��t��
��PE=��[![]() ��4��t��2��
��4��t��2��![]() ��4��t����2]=��
��4��t����2]=��![]() ��4��t��2+
��4��t��2+![]() ��4��t��+2��
��4��t��+2��
�ٵ�N�ڵ�E���ʱ������1+2t��4��t�����t��![]() ��
��
��ʱNE=AO+OE��AN=1+4��t��2t=5��3t��
�ߡ�PNE�ǵ��������Σ�
��PE=NE��
����![]() ��4��t��2+
��4��t��2+![]() ��4��t��+2=5��3t��
��4��t��+2=5��3t��
�������ã�t2��11t+10=0��
��ã�t=1��t=10��![]() ���ᣩ��
���ᣩ��
�ڵ���N�ڵ�E�Ҳ�ʱ������1+2t��4��t�����t��![]() ��
��
��![]() ��2t��5��
��2t��5��
��![]() ��t��
��t��![]() ��
��
��ʱNE=AN��AO��OE=2t��1����4��t��=3t��5��
��PE=NE�é�![]() ��4��t��2+
��4��t��2+![]() ��4��t��+2=3t��5��
��4��t��+2=3t��5��
�������ã�t2+t��10=0��
��ã�t=![]() ��0����ȥ����t=
��0����ȥ����t=![]() ��
��![]() ����ȥ��
����ȥ��
���ϣ���t=1ʱ����PNE�ǵ��������Σ�








