题目内容
【题目】(1)请你画出函数y=![]() x2-4x+10的图象,由图象你能发现这个函数具有哪些性质?
x2-4x+10的图象,由图象你能发现这个函数具有哪些性质?
(2)通过配方变形,说出函数y=-2x2+8x-8的图象的开口方向、对称轴、顶点坐标,这个函数有最大值还是最小值?这个值是多少?
【答案】(1)见解析;(2)见解析.
【解析】
(1)在坐标系中画出函数图象,再从开口方向、对称轴、顶点坐标及增减性阐述其性质;(2)利用配方法把y=-2x2+8x-8化为顶点式,根据函数的性质直接写出开口方向、对称轴、顶点坐标及最值即可.
解:(1)函数图象如图所示:
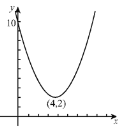
性质有: ①该函数图象的开口向上,对称轴为直线x=4,顶点(4,2). ②当x>4时,y随x的增大而增大;当x<4时,y随x的增大而减小.③当x=4时,y最小值=2.
(2)y=-2x2+8x-8=-2(x-2)2
.该函数图象的开口向下,对称轴为直线x=2,顶点(2,0).
∵a=-2<0,∴y有最大值,当x=2时,y最大值=0.

练习册系列答案
相关题目
【题目】成都和西安两地之间的铁路交通设有高铁列车和普快列车两种车次,某天一辆普快从西安出发匀速驶向成都,同时另一辆高铁从成都出发匀速驶向西安,两车与成都的距离![]() (千米)与行驶时间t(时)之间的关系如图所示.
(千米)与行驶时间t(时)之间的关系如图所示.
t | 0 | 1 | 2 | 4 | … |
S1 | 666 | 546 | 426 | 186 | … |

(1)西安与成都的距离为______千米,普通快车到达成都所用时间为_______小时;
(2)求高铁从成都到西安的距离![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)在成都、西安两地之间有一条隧道,高铁经过这条隧道时,两车相距74千米,求西安与这条隧道之间的距离.