��Ŀ����
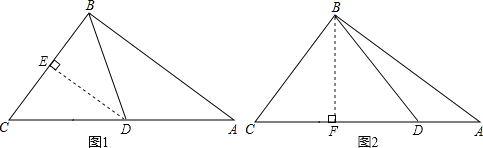
����Ŀ����ͼ����Rt��ABC�У���ABC��90�㣬AB��8��BC��6����DΪAC���ϵĶ��㣬��D�ӵ�C�������ر�CA���A�˶������˶�����Aʱֹͣ�������D�˶���ʱ��Ϊt�룮��D�˶����ٶ�Ϊÿ��1����λ���ȣ�

(1)��t��2ʱ��CD�� �� AD�� ��
(2)��tΪ��ֵʱ����CBD��ֱ�������Σ�˵�����ɣ�
(3)��tΪ��ֵʱ����CBD����BD��CDΪ�ĵ��������Σ���˵�����ɣ�

���𰸡���1��2��8����2��t��3.6���10�루3��t��6���7.2��ʱ
�������������������1������CD=�ٶ���ʱ����ʽ���㼴�ɵý⣬���ù��ɶ�����ʽ���AC���ٸ���AD=AC-CD�������ݽ��м��㼴�ɵý⣻
��2���֢١�CDB=90��ʱ��������ABC�������ʽ���㼴�����BD��Ȼ�����ù��ɶ�����ʽ���õ�CD���ٸ���ʱ��=·�����ٶȼ��㣻�ڡ�CBD=90��ʱ����D�͵�A�غϣ�Ȼ�����ʱ��=·�����ٶȼ��㼴�ɵý⣻
��3���֢�CD=BCʱ��CD=6����BD=BCʱ������B��BF��AC��F�����ݵ������������ߺ�һ�����ʿɵ�CD=2CF�����ɣ�2���Ľ��۽��
�����������1��t=2ʱ��CD=2��1=2��
�ߡ�ABC=90����AB=8��BC=6��
��AC=![]() =10��
=10��
AD=AC-CD=10-2=8��
�ʴ��ǣ�2��8��
��2���١�CDB=90��ʱ��S��ABC=![]() ACBD=
ACBD=![]() ABBC��
ABBC��
��![]() ��10BD=
��10BD=![]() ��8��6��
��8��6��
���BD=4.8��
��CD=![]() =3.6��
=3.6��
t=3.6��1=3.6�룻
�ڡ�CBD=90��ʱ����D�͵�A�غϣ�
t=10��1=10�룬
����������t=3.6��10�룻
�ʴ�Ϊ����1��2��8����2��3.6��10�룻
��3����CD=BCʱ��CD=6��t=6��1=6��
��BD=BCʱ����ͼ2������B��BF��AC��F��
��CF=3.6��
CD=2CF=3.6��2=7.2��
��t=7.2��1=7.2��
����������t=6���7.2��ʱ����CBD����BD��CDΪ�ĵ��������Σ�